Discontinuous chords in wood framed building @ dormers 3

[redtiger]

Hello,

I am working on a new wood framed building. There are several dormers where the double top plate will have a discontinuity. Please see the attached sketch.

Based on diaphragm design, the chord force is around 2.5 kips. My question is the following, how do I connect the plates at these locations. My first idea was to install a steel frame at these openings, weld a strap to the end of each steel post and nail the other side of the strap to the next continous double plate.

Any other ideas would be greatly appreciate it.

Regards

 

[KootK]

Your sketch assumes flexural deflection. Diaphragms have significant shear deflections so that 3x rotation, and your sketch, isn't all that meaningful or correct...Even with your not-correct flexurally deformed diaphragm,

While I agree that wood diaphragms undergo significant shear deformation, the assertion that my flexural analysis is meaningless or incorrect is seriously flawed.

1) Just because shear deformations exist, that's no reason not to bother looking at flexural stresses strains.

2) If flexural stresses and strains are not important or relevant, then why bother with chords? We certainly don't bother with them to deal with shear deformation.

3) Shear deformations are additive to flexural deformations. As such, you'll see the 3X strain shown in my sketch and then some more drift as a result of shear deformation.

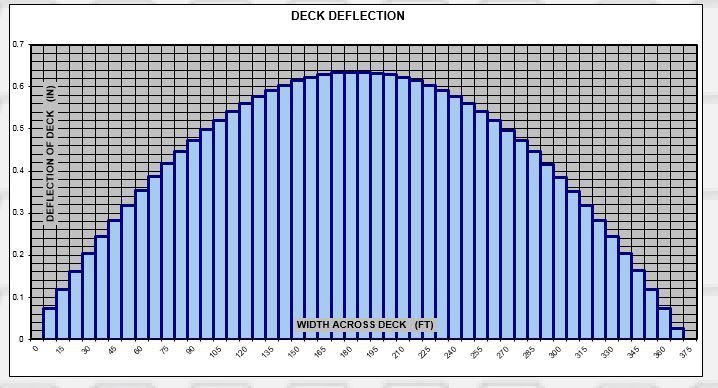
you'd still work backwards to find a half-roof diaphragm stiffness that would limit that arc. I use the term back-calculating to suggest that you'd start with the limit on deflection and then back-determine the necessary diaphragm stiffness to accomplish that.

Ok. But you're calculating the arc length incorrectly by ignoring the role that diaphragm depth plays. So your back calculation, by merely enforcing a drift limit, isn't enforcing any particular limit on in-plane diaphragm strain. Less drift begets less strain, obviously, but strain is not quantified by your suggested procedure.

For a usual range of 3-story wood framed buildings, that drift limit really minimizes the resulting arc length of the eave edge.

While I agree with the conclusion, I still contend that your estimation of the resulting arc length is flawed as I discussed previously.

Wood is a very VERY forgiving material in construction and the use of a half diaphragm in this particular case, just isn't that big of a concern. I've even done this on other designs and with no problems.

I agree and have acknowledged as much several times here. I do a version of the same thing myself, sometimes even in steel. This expanded discussion is theoretical only in my opinion. That said, I think that there's presumption in suggesting that a short history of successful performance represents a glowing endorsement of the half diaphragm method. Roof diaphragms essentially never have problems. And that includes all of the real world diaphragms that have discontinuous chords, no heel blocking, no ridge blocking, and no properly detailed colledtors. They work because these systems are often heavily redundant, not because of the spiffy tricks of structural engineers.

What Mike says above, adding a collector of sorts to the top of the dormers, could be considered as well...just more cost and to accomplish what, though.

Sure. I was the first to suggest this strategy up at the top.

Another alternative would be to step your chord 4'-3" back up into the roof at the dormers and provide a chord segment there effectively detailed to lap with the wall plates.

I would say that:

1) In theory, it accomplishes a design that gives proper credence to realistic deformations and strain compatibility. It also produces a design in compliance with the methods that seem to be becoming the state of the art in our industry.

2) In practice, it probably accomplishes nothing at all except, perhaps, to spare the diaphragm some localized damage at the re-entrant corners of the notch during a very extreme event.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[JAE]

Your flexural only sketch was incorrect in that it attributed all of the deformation to flexural behavior. Thus my assertion that your drawing was incorrect, was correct.

You state that "my estimation of the resulting arc length is flawed". Perhaps I haven't done a rigorous analysis of an actual diaphragm...but my assertion that the arc length results in small strains is correct regardless of the share of deformation between flexural or shear based deflections.

I even said that even at 3 x the deflection (your incorrect assertion of a flexural only deformation) the strains were small...that is still true.

Providing a chord (like (2) 2x6 top chords) isn't going to change the strains in other elements of the diaphragm or dormers anyway. The total deformation of a diaphragm isn't affected by the chords all that much as a larger proportion of your diaphragm deformation is shear-based. The chord does nothing to reduce that.

This is getting a bit tedious so I'm signing off this thread. All I'm saying is that you could use a half diaphragm successfully. I've done it before. It works.



Check out Eng-Tips Forum's Policies here:
faq731-376

 

[jdgengineer]

On a side note, as an engineer I would shy away from the argument "I've done this before and didn't have any problems therefore it's not a problem". That is a contractor argument not an engineering one. As we all know we design lateral forces (wind & seismic) for long return period events. It's highly likely the structure has not been subjected to full code design forces yet. Even for more predictable gravity loading it's likely the structure hasn't seen its full live load as those are typically designed for extreme loading scenarios that the structure may only see a few times (or never)

The code has implied safety factors associated with design procedures which translates to maximum acceptable probabilities of collapse. Just because the structure doesn't have problems doesn't mean it meets the intent of the code provisions or acceptable probabilities of collapse potential.

Food for thought -- In SF Bay Area I could have designed structures without any seismic design principles and not have had any problems for past 27 years. Not exactly something I would take comfort in.

 

[RFreund]

TLDR for the most part, but it seems like Kootk and JAE might be misunderstanding each other and saying the same thing.

I think JAE is saying that you would need to design the LFRS such that your drift displacement is small, so that even when you project this displacement out to the outside edge of the dormers it is a small strain at this point.
KootK is saying well when you project it out it is larger than what you had calculated at the point you calculated it at.
Both seem to be saying that:
Unless your diaphragm that was "going along for the ride" was much much deeper than your diaphragm "doing the work" you're probably ok. And if it was much much deeper then you would violating diaphragm ratio limits.

And also saying that it would be nice to have a better load path like the blocking and strapping mentioned by M^2.

EIT

http://www.HowToEngineer.com

 

[KootK]

The code has implied safety factors associated with design procedures which translates to maximum acceptable probabilities of collapse. Just because the structure doesn't have problems doesn't mean it meets the intent of the code provisions or acceptable probabilities of collapse potential.

I agree strongly with this. I would, however, argue that similar reasoning should lead one to conclude that wind loads are just as important as seismic loads. All of the elements of risk and reliability are already baked into the cakes that are our code specified wind and seismic loads. Beyond that, load paths are load paths and strain is strain.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[jdgengineer]

I agree KootK. Better or worse I'm always in high seismic so a wind only approach never comes up. I agree following the intent of the code,good detailing practices are important for both.

 

[KootK]

Your flexural only sketch was incorrect in that it attributed all of the deformation to flexural behavior. Thus my assertion that your drawing was incorrect, was correct.

I was interested in studying in-plane axial strains in the diaphragm. That was the scope of my analysis. Given a particular diaphragm load, flexure contributes to in-plane axial strain and shear does not. Therefore, my diagram was 100% correct for the purpose for which I created it.

If one starts with a limit on drift and some of that is eaten up by shear does that mean that there will be less drift going into the flexure bucket? Yeah, of course. Does that invalidate my analysis of the fexural strain component? Not at all. Note that nothing about my sketch contradicted the notion that shear contributes to diaphragm deformation. I simply did not choose to study that nuance. If you want a sketch that does speak to shear deformation, I suggest that you create one of your own.

.but my assertion that the arc length results in small strains is correct regardless of the share of deformation between flexural or shear based deflections. I even said that even at 3 x the deflection (your incorrect assertion of a flexural only deformation) the strains were small...that is still true.

You seem to be getting stuck on the magnitude of the strain. I don't care about the magnitude of the strain. In almost every one of my posts here, I've repeated clarified that:

1) I, like you, think that the magnitude of the strain is small.

2) I, like you, suspect that the strain is not a serious concern in practice.

We do not need to continue faux-debating whether or not the strain is small or whether or not it's a serious issue in practice. We've agreed on that from the start.

Providing a chord (like (2) 2x6 top chords) isn't going to change the strains in other elements of the diaphragm or dormers anyway. The total deformation of a diaphragm isn't affected by the chords all that much as a larger proportion of your diaphragm deformation is shear-based. The chord does nothing to reduce that.

So why bother with chords then? Is the state of the art really that much in the wrong? And I would argue that how much of a diaphragm's response is shear based is very much a function of the diaphragm aspect ratio. And, in fact, by going with the half diaphragm approach, one is creating an analytical diaphragm in which the influence of flexure is actually increased relative to the influence of shear. In the OP's example, it appears that we might even be getting close to code limits in that regard.

This is getting a bit tedious so I'm signing off this thread.

I'm sorry that you feel that way. I've been enjoying the discussion and was hoping to tease a bit more understanding out of it yet. However, years of experience has taught me that you're first and foremost a practical fellow. And you prefer not to get bogged down in technical minutia, which I get.

All I'm saying is that you could use a half diaphragm successfully. I've done it before. It works.

Yes, and I have not really disputed that. I merely mentioned a slight concern, of my own, for strain beyond the designated structural diaphragm. And I feel that I've done a reasonable job of legitimizing that concern here.


I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

KootK is saying well when you project it out it is larger than what you had calculated at the point you calculated it at.

Exactly right. At least that's what I started with.

it seems like Kootk and JAE might be misunderstanding each other and saying the same thing.

There is one fundamental disagreement that should not be overlooked. We clearly disagree on how chord/diaphragm strain should be calculated. I think that diaphragm depth factors into it in a big way. JAE doesn't think that it comes into play at all (my interpretation of his comments). That's kinda huge.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[JAE]

I think that diaphragm depth factors into it in a big way. JAE doesn't think that it comes into play at all

KootK that is not really representative of what I said. I don't believe that it doesn't come into play in the derivation of the strains at the outer edge.

What I said was that if you design a half-diaphragm the resulting design checks (which you correctly advocate) can determine that the outer arc strains on the eave are under control, or limited.

The true diaphragm drift is a combination of shear deformation (roughly shown here):

AND Flexural deformation - that you illustrated in your sketch above.

I commented that your sketch was not really correct - and it is not - it ONLY shows the flexural deformation of the diaphragm and ignores the significant share of shear deformation.

You provided that flexural deformation sketch to support the notion that the depth of the diaphragm affects the resulting arc length at the eave, which it does - but not 100% as you implied.

I agreed that there was additional strain at the outer eave but again - not due to 100% of the flexural deformation (the 3 times value you showed) but the TRUE eave strain would be somewhere below that amount.

The influences of both are present. For most diaphragm sizes in wood construction, the shear deformation tends to be more influential in the total deformation than flexural but then I even conceded that if the 3 times amount you incorrectly showed was present, you'd still have small amounts of strain in the chord, which you agreed.

I see that this discussion seems to be devolving into an "I can out-quote you last" so I'll concede the thread and let you have your way with your quote machine. But my really only point here is that a half-diaphragm can be designed to control drift in buildings and with most simple wood framed structures (like apartment buildings) the resulting strains at the outer edge are (under service conditions - not extreme seismic conditions) manageable and don't result in long term issues.

jdgengineer - I agree that a contractor statement depending on past results isn't purely a true engineering statement but we were talking about serviceability issues (cracks at the dormers) not life safety issues.
28 years is a pretty long time to see results, even with wind...but you're correct - it wasn't 50 or 100 years.



Check out Eng-Tips Forum's Policies here:
faq731-376

 

[jdgengineer]

My main concern with the diaphragm would not really be in the left to right direction, I would be more concerned in the up and down direction to make sure that there is adequate load transfer mechanism to the shearwalls between the dormers. In the left to right direction, I tend to agree with you all the half diaphragm approach works as long as the other half of the diaphragm is detailed well to go along for the ride. This type of approach can be commonly used in concrete diaphragms and is shown well in the "Seismic Design of Cast-in-Place Concrete Diaphragms, Chord, and Collectors" (NEHRP Seismic Design Technical Brief No. 3.

Personally, I would still put in the line of strapping as Mike mentioned at the top of the dormers. If you all don't then great, you can tell the contractor you are more economical . Wouldn't change my approach, personally.

To follow-up on the 28 year comment. I don't agree. In ASCE 7-10 Category II structures are designed for 700 year MRI wind event, and Category III and IV are designed for 1700 MRI wind event. In my opinion, I don't believe 28 years is adequate time to say the structure is "tested". If the reference was in regards to my comment about the SF Bay Area, the point I was trying to make was that we have not had a major earthquake since 1989. Therefore, you could have ignored seismic detailing completely and not have had a problem since 1989. That time spans the career of a lot of engineers, but I think we could all agree that the 27 years is not adequate time to say the structure is tested in a seismically prone area.

I'm not trying to be argumentative, sorry if I am coming across that way.

 

[jdgengineer]

Based on the conversations, above I'm sure you will all laugh, but for larger dormers we do try our best to tie the structure together. Here is example with HSS "transfer post" essentially post cantilevered from low roof diaphragm to try and grab and tie together upper dormer area. Chord continuity is not great as there is a vertical jog, but it's the best we could do. Story drift was checked including deflection of HSS post. We also had strapping at the top of the dormer as Mike suggested (in our case it was a continuous steel ridge that was already there). I don't think this detail would be necessary for the type of dormers shown in the roof plan, unless you only had shearwalls on one side of the plan and were trying to preserve collector continuity all the way across.

 

[KootK]

I do indeed agree with most of that.

I commented that your sketch was not really correct - and it is not - it ONLY shows the flexural deformation of the diaphragm and ignores the significant share of shear deformation.

I do not accept your assessment that my sketch was incorrect. It was utterly correct with respect to what I was attempting to convey: the nature of flexural strain here. My diagram was, perhaps, incomplete with respect to what you wanted to see acknowledged: the influence of shear deformation on felxural strain in a limited drift scenario. How about that?

not due to 100% of the flexural deformation (the 3 times value you showed)

My sketch did not say that 100% of the drift manifested itself as flexural deformation. My sketch said that eave flexural strain would be 3x half diaphragm flexural strain. And that is true.

I see that this discussion seems to be devolving into an "I can out-quote you last" so I'll concede the thread and let you have your way with your quote machine

Please don't be put off by the quoting. I know that it feels like a personal attack at times (that's how ego endowed creatures are built) but I really just do it because it's an efficient way for me to thoroughly and systematically process all of the points of contention. I'm an engineer after all. I find that when others don't quote, that's when in depth discussions really devolve into pitiful messes.

We've known each other for a while now. I would hope that you would think better of me than to assume that I'm engaging in some kind of petty "quote arms race". If I bother to say something, it's because I feel that it has substance. If you want to be done here, then be done. You can't expect me to stop discussing things with you when you're still discussing them with me however. I like it after all.

While I suspect that you will not be interested, I still think that there's an important point to be resolved regarding the calculation of chord diaphragm strain. Given my druthers, I would like to:

1) Have you supply your calculation for the 1/64" elongation number.

2) I'll do my best to produce a calculation doing it my way.

That way, we can objectively attempt to resolve something meaningful. How about:

1) 100 ft X 30 ft diaphragm.
2) 3" midspan deflection based on a parabolic flexural curve.
3) You specify the percentage of deflection attributed to shear based on your original calc.

I'll invest the time if you'll share your stuff.



I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

Based on the conversations, above I'm sure you will all laugh, but for larger dormers we do try our best to tie the structure together.

Hell no I'm not laughing. I'm jealous that your market can support high quality structural engineering solutions. I actually interviewed with a few firms in California last spring. And my very specific intent was to be able to practice in a region where:

1) Folks know good structural when they see it and;

2) There's half ways decent regulation and;

3) There's at least a modicum of hope for getting paid for #1.

I practice in a hopeless backwater in this regard.

Thanks for sharing your solution.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.