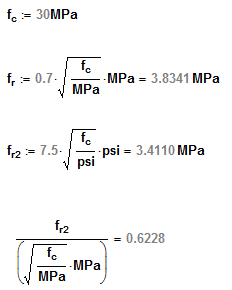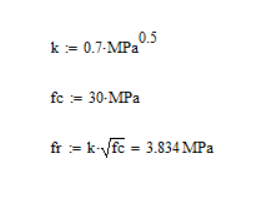Continue to Site

Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in
  • Congratulations GregLocock on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

DISPLAYING UNIT CONVERSIONS IN MATHCAD EQUATION 3

Status
Not open for further replies.
scottwins

scottwins

Mechanical
Mar 10, 2017
5
Is there a way to display the unit conversion factors within the Mathcad equation without Mathcad calculating the conversion twice? I use Mathcad pretty extensively and many times I need to present calculations via a teleconference and I always get questions on the units and equations don't appear right. I know Mathcad calculates them in the background and I always state that but is there a way to display them just so the equation looks correct? For instance in the Formula, Torque based on Inertia and Time: Dynamic Torque=((Wk^2-inertia)(RPM))/((308)(time)) with 308 being the unit conversion factor.

Thanks in advance,
Scott
 
Replies continue below

Recommended for you

Sort by date Sort by votes
If you put the correct unit in, Mathcad will happily do the conversion in the background as the OP said. Suggest using a text box next to the Mathcad formula to show the formula with conversion factors.
 
Upvote 0 Downvote
Sorry, mis-read. In Mathcad, unit conversion factors should not even be in the equations to start with, if you are actually using units.

Perhaps you can post that part of your sheet.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
... Dynamic Torque=((Wk^2-inertia)(RPM))/((308)(time)) with 308 being the unit conversion factor.
Click to expand...

If your clients need the "old" equation, then StevenAL's suggestion to use a text box is the way to go, rather than corrupt the calculations.

<rant=ON>

As long as you are using variables without units that are supposed to have them, you will always be fussing with extra "308" factors and confusing your clients.
When you get tired of micro-managing the units for MathCAD, just let MathCAD do the units for you. Start by giving all of your input values units.

Note that your 308 is inexact and missing some decimal places, like many others such as "g=32.2" and the divisor in the equations for power "5252" or "63025" or "1713" or "229" depending on whatever machine you're working on. Input the units properly, and you don't need any of this stuff. Forcing MathCAD to use them in the calculation adds error into an equation that does not need it. MathCAD - by design - handles units in the background whether you are using US, SI or CGS systems. It's one of the things I love about it, and I guess one of my pet peeves to see users who haven't discovered/accepted this.

<rant=OFF>
Thanks for reading

STF
 
Upvote 0 Downvote
Another option is to have both Mathcad and the old equations live, side by side. The old equations can be used in the context of Mathcad using the same variables, with the exception that the old equation will have the variables normalized to the unit system in the equation, so you'd use "time" as the variable for both equations, but the old equation would have time/hr, or whatever.

What's cool about this is that if something changes, the old equation should give you the same answer as the Mathcad approach.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
I don't use Mathcad, but I'm interested in how it handles formulae with constants with implied units, like tensile strength of concrete = k*f'c^0.5.

Do you assign units to the constant, and if so does it recognise sqrt(stress) as a valid unit, or is it handled differently?

Doug Jenkins
Interactive Design Services
 
Upvote 0 Downvote
Most of the stuff I do, I avoid using empirical formulas.

But, for those that do exist, it's basically as I outlined above. You define your variables normally, with their correct units. Inside the empirical equation, you normalize the units to what's required for the formula, and then tack on the imposed units. That's my approach, and it allows you to use whatever units suit you outside of the empirical stuff, but retains all the essential information, particularly what units are required for formulas, without having to resort to text boxes to document things.

By retaining the units within the equations, it makes it more turnkey, which is particularly important if you come back 6 months later and try to use it again.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Yeah that is what I had figured ( put formula as text, next to Mathcad formula) but was wondering if there was another way. I know what Mathcad is doing but others don't and I always have to explain it. It just makes discussion longer when I have to explain what Mathcad is doing rather than if equation is properly displayed showing unit conversion factor within equation.
 
Upvote 0 Downvote
" equation is properly displayed showing unit conversion factor within equation"

ugh, not in my definition of "properly" ;-) but customers will be customers...

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Doug - Mathcad understands units. It knows that there are 12 inches in a foot, 25.4mm in an inch, etc. The number of units built is substantial and you can define any units you want. If you tell it that the variable F sub c is defined as 30,000 psi it shows psi as you type it and knows what to do with it (as long as it has the unit psi either built in or user defined). Then, if for instance you ask for the results in MPa it gives you the answer in MPa as long as the unit MPa is defined. If you want to show a unit that does not exist, you can define one, like Drinks = 1.0 ounce and Whisky = 12 Drinks. You can define a unit that has no units, like Moon = 1.0 and then include it in an equation by multiplying the equation my Moon which shows the unit but does not change the value of the result.

Etc
 
Upvote 0 Downvote
@IDS:

The problem with "empirical formulae" such as your example where the tensile strength of concrete is given by:

f'ct = 0.36 * (f'c)^0.5

is that they are dimensionally inconsistent, and they only work if you enter the parameters in the required units. (The above example is from AS 3600, and gives the tensile strength in MPa if you enter the compressive strength in MPa - clearly it doesn't work if you enter the compressive strength in any other units, so the corresponding "empirical" relationship in American codes would use a different factor to obtain the equivalent "empirical fit" between compressive strength and tensile strength.)

My preferred approach for handling "empirical formulae" in dimensionally-aware software such as Mathcad is to define all parameters with their correct units, then whenever a dimensional parameter appears in an empirical formula, you divide all parameters by their units, making all parameters non-dimensional, and then finally multiply the whole expression by the implied units. E.g. for the above example, I would write:

f'c = 32 MPa
f'ct = 0.36 (f'c / MPa)^0.5 MPa

The first expression means that Mathcad "knows" that f'c carries units of "stress" or "pressure", and it will be quite happy whether you define it in MPa, psi, kgf/cm2, or whatever.

In the second expression, dividing f'c by its implied units makes it unit-less; so the expression can be evaluated correctly; multiplying the whole expression by MPa means that the solution for f'ct carries the required units.

If I want to know what the tensile strength is in psi or kgf/cm2, I just ask Mathcad to present the solution in alternative units of my choice. (This is very handy when doing a calculation to Australian or European codes, but needing to be understood by an American reviewer, for example.) If I want to know the tensile force carrying capacity of my concrete member, I multiply f'ct by the area of the section (which again carries appropriate units, whether it is square millimetres, square inches, or acres), and I can get the tensile capacity in kN, kips, kgf, or whatever.



 
Upvote 0 Downvote
"Does it recognise sqrt(stress) as a valid unit?"

Yes it does. The unit will the stress unit of your choosing raised to the 0.5 power, probably not what you're looking for. I suspect the k value isn't really unitless, and carries a unit that also looks like stress raised to the 0.5 power.
 
Upvote 0 Downvote
According to the web, the two formulas are:

0.7*sqrt(fc) in SI units
7.5*sqrt(fc) in US units

However, when I solve for coefficient for the SI unit case using the US case, the coefficient is 0.62, not 0.7; 10% or so might not be a big deal, but this seems a bit sloppy and annoying.
concrete_eo3jpl.gif


TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Here's how I would do it. No dividing and multiplying by units needed.
2017-09-26_11_22_18-Mathcad_-_Untitled_1_ylbedc.png
 
Upvote 0 Downvote
@IRstuff:

The reason that the US and metric formulae yield different answers is that it's an empirical fit, and dimensionally inconsistent - hundreds of test samples have been plotted onto a graph, and a curve of best fit has been applied. Presumably, the committees responsible for the two expressions have used different subsets of data, or possibly are using different definitions of the strength (i.e. is it mean strength, or mean minus 1 x SD, or mean minus 3 x SD, or ...)

When you think about it, there is no theoretical basis for why the tensile or shear strength of concrete would be proportional to the square root of the compressive strength, it just happens to be a good fit for design purposes.

 
Upvote 0 Downvote
No, I get that, I'm just not grasping why they aren't numerically consistent with each other; 0.7 is noticeably far away from 0.62. It's not a difficult math problem.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
IRstuff - I can only guess that they didn't want to imply that the empirical factor had a higher precision than 1 significant figure, but for some reason they didn't want to round down to 0.6, so they rounded up to 0.7, but I agree, either 0.6 or 0.62 would have been better. FWIW, the Australian codes use 0.6.

Regarding adding the units in the empirical code formula, I know Mathcad handles units, but as has been pointed out you have to be careful how you do it. I just happen to have done a blog post on how to do it with my units aware Excel spreadsheet (Working with implied units), so I was interested how Mathcad would do it. Thanks for the detailed responses above; I'll update the blog post with some more alternatives.

Doug Jenkins
Interactive Design Services
 
Upvote 0 Downvote
@IRstuff again:

The scatter in the empirical relationship is pretty wide, so it is not surprising that different codes use different expressions. Also, you need to be clear whether the strengths which are derived are flexural tensile strength or uni-axial tensile strength, and whether they are "typical" mean strengths, or lower-bound "characteristic strengths" - the codes will use different design factors depending on whether they are using a "typical" or "lower bound" strength.

E.g. take a look at this page:
"Relation Between Compressive and Tensile Strength of Concrete"

Numerical Relationship

It is expected that these two types of strengths are closely related, but there is no direct proportionality. It is noticed that with the increment of compressive strength, the tensile strength is also increased but at a decreasing rate.

A better correlation is found between the various measures of tensile strength and the square root of the compressive strength. A number of empirical formulae connecting ft and fc´ have been suggested, many of them of the following type:

ft = k (fc)^n

where k and n are co-efficients. Values of n between ½ and ¾ have been suggested. The former value is used by the American Concrete Institute, but Gardner and Poon found a value near the later, cylinders being used in both cases. Probably the best fit overall is given by the expression:

ft = 0.3 (fc)^2/3

where, ft is the splitting strength, and fc´is the compressive strength of cylinders, both in megapascal. If the stress is expressed in pounds per square inch the co-efficient is replaced by 1.7. The above expression was suggested by Raphael. A modification of Oluokun is

ft = 0.2 (fc)^0.7

where the strength are in megapascals; the co-efficient becomes 1.4 in psi.

An expression used in British Code of practice BS 8007:1987 is similar, namely

ft = 0.12 (fc)^0.7

Clearly, these expressions can't all be "right", and they are clearly empirical fits as they dimensionally inconsistent, but they're all "good enough" for design purposes. (As long as you use all of the appropriate design rules from the respective design code - for example, a code which predicts a higher tensile strength for concrete will probably adopt a larger "material reduction factor" in the design rules.)


 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

weikequ
  • Question
Things you love/hate with mathcad 1
Replies
17
Views
6K
robertdyas1972
R
271828
  • Locked
  • Question
Mathcad Prime - subscript . and unit font 1
2
Replies
22
Views
1K
samirhayatkhan
samirhayatkhan
yuriy_biks
  • Locked
  • Question
&quot;This value must be a scalar&quot; issue in the FOR loop Mathcad Prime 9 1
Replies
12
Views
614
3DDave
3DDave
julian89
  • Locked
  • Question
Trilinear interpolation in mathcad prime?
Replies
3
Views
442
bkal
bkal
WARose
  • Locked
  • Question
Copying from MathCAD to Word
Replies
14
Views
916
dik
dik

Part and Inventory Search

Sponsor

Back
Top Bottom