distributed reaction forces for overhanging rigid load

[yorp15]

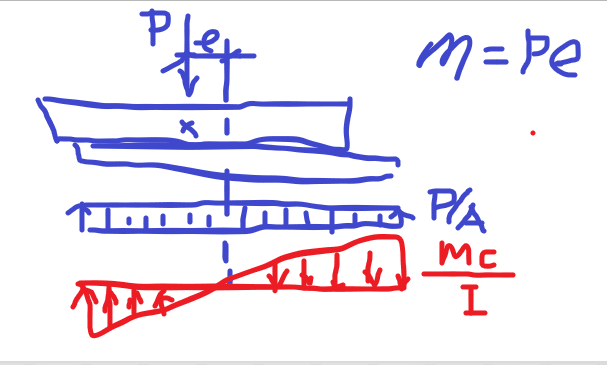
I'm analyzing a pallet holder where the load (mass = m, length = L, assumed to be a rigid body) rests between the top and bottom plates (it's just slotted in there, the top plate isn't weighting the load down in any way). The load is also secured laterally with a slight slip allowed but just looking at the vertical load case at the moment. See diagram below. The load is able to overhang forward of the edge of the plates (overhanging length = a, supported length = b = L-a). To start with, I'm assuming the load has uniform mass distribution (it actually is non-uniform and I know the CG location, however I'm already having trouble with a uniform distribution so I'd like to start there).

Can someone help me with the FBD for the load? It seems like a simple problem however I'm having trouble convincing myself of the correct approach.
(Distributed loads shown as thin lines with the sum shown as a thicker line. For ease of visualization, the weight of the load is color coded with unsupported and supported lengths in green and blue respectively.)

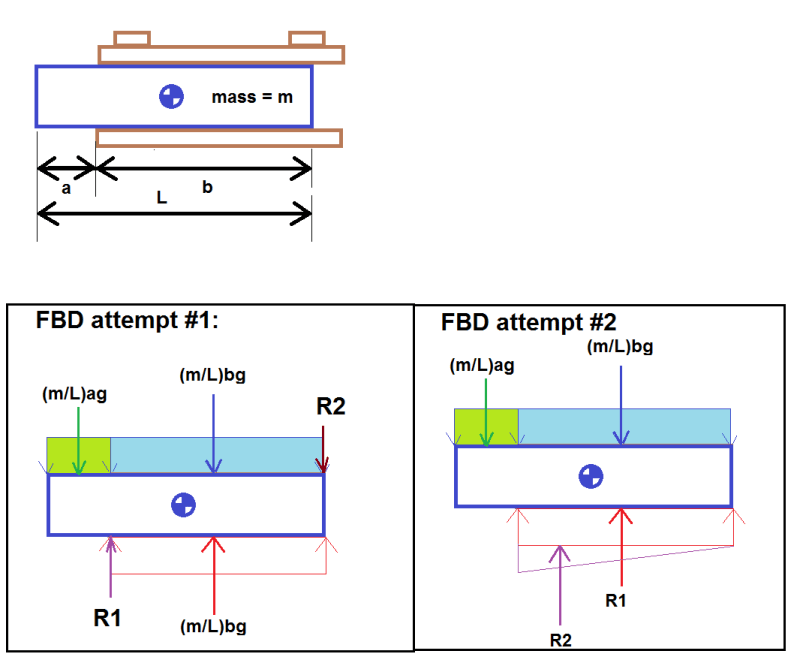
Attempt #1:
[ul]
[li]My first thought was that the weight of the supported length is directly reacted by a normal force (i.e. (m/L)*b*g in both directions). [/li]
[li]The weight of the unsupported length is then reacted by a point load at the corner where it overhangs (R1).[/li]
[li]But then there's an unbalanced moment. I've decided that this would be reacted by a point load coming from the upper plate onto the aft end of the load (R2).[/li]
[li]The other option for reacting the unbalanced moment could come from the lateral restraint, however because the slip in the lateral restraint is larger than the clearance between the load and the top plate, I'm assuming this isn't the case.[/li]
[/ul]

Attempt #2:
[ul]
[li]The normal force is 'skewed' towards the overhanging side of the load supported length is still primarily reacted with a normal force, but now it's no longer equal to the supported length's weight.[/li]
[li]R2 located at 2/3*b from the right hand side. R1 located at 1/2*b [/li]
[/ul]

Do either of these seem reasonable? Or is there something else to consider?

Then, my real load has a non-uniform mass distribution with the CG still between the plates but further towards the forward (LHS in the diagram) side. I could adapt either attempt #1 or #2 by idealizing the weight as a point load at the CG to calculate the reactions, however adapting attempt #1 would involve having to assume/calculate the supported mass & CG vs unsupported mass & CG.

 

[r13]

Isn't it looking like this? You need define the full length of the holder to calculate support properties.

 

[yorp15]

Oh I see what you're getting at, although your diagram confused me for a while. Do you mean:

i.e. the reaction is a normal force plus a moment caused by the eccentricity, which can be swapped into a couple (R1) acting about the mid-point of the contact area.
M = mg*e = R1 * 2b/3

I think at one stage I was considering this but can't remember why I discarded it. Seems legit.

 

[r13]

Yes, don't hang over and get confused by the contact area only. Think it as eccentrically loaded footing, or base mat of retaining wall, what you will do? Then do the same. It is still holding true, if the load is within middle third of the base, then there is no tension/uplift.

 

[CANPRO]

I think retired13’s approach is reasonable, depending on how accurate you want/need to be.

Ultimately it will be a function of the stiffness of both the top and bottom supports as well as the load (rigid assumption noted). I think the supports would have to be fairly “soft” to get the pressure distribution sketched above.

 

[r13]

You can analyze it as beam on elastic foundation, but I wouldn't get into that trouble. For resultant force remain within the middle third, the top support would not in the play (it stays the state it was in).

 

[rb1957]

and you'll know you're heading for trouble if the (tension) peak of the bending (triangular) exceeds the (compression) of the UDL.

you can't have the bending tension exceed the UDL compression. You can rejig the bending distribution, but it's more trouble than it's worth and "disaster" is only moments away.

another day in paradise, or is paradise one day closer ?

 

[HTURKAK]

The resultant reaction of the base will coincide with the C.G. of the load. If we assume the load is rigid body , the reaction of the base will be triangular distribution ( if e ≥ L/6 ).

thread507-414201


I think some questions have a certain period like merry- go -round.

 

[r13]

HTURKAK,

Your equation is very handy for e>L/6, but not correct for this case. This guy has a sandwich system, once rotation starts, the top lid will restrict the rotation. From that point on, the stress distribution is getting very messy.

 

[rb1957]

doesn't the upper lid simplify things ? the moment comes out as a (compression/contact) couple between the two sandwiching plates ?

another day in paradise, or is paradise one day closer ?

 

[HTURKAK]

This guy has a sandwich system, once rotation starts, the top lid will restrict the rotation. From that point on, the stress distribution is getting very messy.

The top plate will start to resist to overturning of rigid load , after a≥ b or a≥ (L/2). If a ≤ (L/2) , the mentioned equation is valid.

For the case a≥ b , the approach could be similar to socket analysis of P.C. column. For refined analysis , elastic analysis should be conducted.

 

[r13]

HTURKAK,

When the top plate starts to resist the moment, its base is shortened to the contact surface with the medium, not the ground. However, the problem is getting messier by the stress on the top plate will be transmitted/distributed to the connectors/linkage of the top and bottom plates, thus increase the stress in the bottom plate. Note the medium is loosely (not rigidly) connect to the plates, the contact pressure is much more complicate than the method you addressed.