Hello
I have a question on eccentric load cases as below.
Would anyone could help me with this?
[link Loading of the connection by a force inclined to the contact surface not running through the connection gravity centre.][/url]
[link Derivation of Bolted Joints When Load Is Parallel to the Axis of Bolt - Design of Machine][/url]
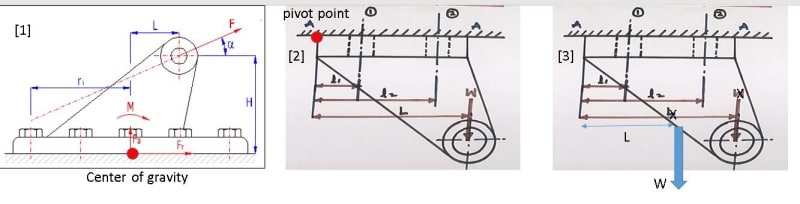
[1] M=Fr*H - Fa*L : Why do we have to substract Fa*L? I thought theses two components has to be added together. ([1] & [2] : When calculating Moment, [1] is based on the point in the middle of the plate [2] is based on the pivot point. Is it because of Force direction? Can I assume the lever arm starts from the middle of a plate, if force direction is diagonal? (if the bolts are symmetrically installed on a plate)
[3] if W location is between the two bolts, does the equation "wt2=(W*L)/2/(l1^2+l2^2)xl2" still valid? . I actually think so.
Thank you
I have a question on eccentric load cases as below.
Would anyone could help me with this?

[link Loading of the connection by a force inclined to the contact surface not running through the connection gravity centre.][/url]
[link Derivation of Bolted Joints When Load Is Parallel to the Axis of Bolt - Design of Machine][/url]
[1] M=Fr*H - Fa*L : Why do we have to substract Fa*L? I thought theses two components has to be added together. ([1] & [2] : When calculating Moment, [1] is based on the point in the middle of the plate [2] is based on the pivot point. Is it because of Force direction? Can I assume the lever arm starts from the middle of a plate, if force direction is diagonal? (if the bolts are symmetrically installed on a plate)
[3] if W location is between the two bolts, does the equation "wt2=(W*L)/2/(l1^2+l2^2)xl2" still valid? . I actually think so.
Thank you

