ENGUCR
Structural
- Sep 23, 2017
- 37
Hi,
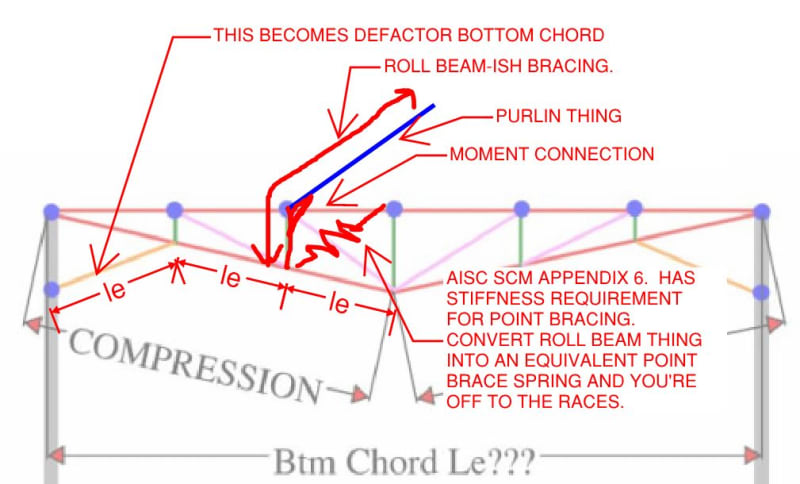
I need a bit of advice on the selection of effective length for the compression capacity calculation of bottom chord of a truss(double inverted) when there is a mixture of tension and compression in this chord member. Please see the attached axial force diagram. What length should I use for this out of plane buckling? is it the entire length of chord member or the segment length of the compression part?
Tx in advance
I need a bit of advice on the selection of effective length for the compression capacity calculation of bottom chord of a truss(double inverted) when there is a mixture of tension and compression in this chord member. Please see the attached axial force diagram. What length should I use for this out of plane buckling? is it the entire length of chord member or the segment length of the compression part?
Tx in advance