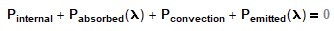Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in

Environmental IR Radiation Entering Ground Equipment 1

Status
Not open for further replies.
Tunalover

Tunalover

Mechanical
Mar 28, 2002
1,179
0
0
US
Guys:
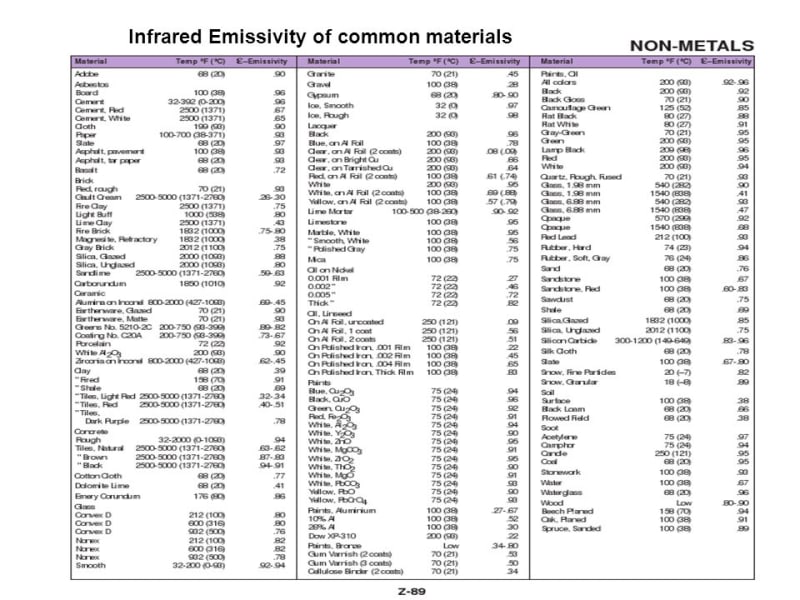
For the IR heat absorbed from a terrestrial environment (but NOT including sunlight), how can I prove/show that the emittance and absorptance of a particular painted or unpainted metal surface are equal for that IR spectrum? I know it involves Kirchoff's Law but Kirchoff's Law is much more than just α=ε (true only for gray bodies).

ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Replies continue below

Recommended for you

Sort by date Sort by votes
Actually, you can include sunlight if you want. The key, as always, is the equilibrium temperature; the object absorbs energy until the emitted energy balances. If something is at a constant temperature, then, by definition, gazinta = gazouta, irrespective of the absortivity or emissivity, i.e., E[sub]in[/sub] = E[sub]out[/sub], the continuity equation, or Kirchoff's Law.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
IRStuff you have "IR" in your name but maybe not in your heat transfer.

A piece of equipment will absorb heat from the UV, IR, and visible parts of the spectrum FROM THE SUN. And it will absorb IR heat from its surroundings. And the box will then reject the internal electronic power dissipation, absorbed solar radiation, and radiation absorbed from its surroundings (as it would in complete darkness) by emitting IR radiation and by convection.

I repeat my question but now cast it as one at night time in complete darkness. Knowing the equipment will absorb IR heat from the surrounding even at night, how can I show that the IR absorptance is the same as the IR emittance for painted metal surfaces that are highly non-gray (and definitely not black)?

ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Upvote 0 Downvote
Again, an equilibrium surface temperature means input energy equals output energy. It does not matter how the energy comes in and it does not matter how the energy goes out. Every energy transport mechanism into an object is dependent on the temperature of the object's surface and by extension, the temperature of the interior, so, if the surface temperature of the object is constant, then the heat flows are constant. Any imbalance in energy flow results in a temperature change. For instance, if someone decided to turn on a heater inside the box, then the interior temperature must rise, causing the surface temperature to rise until the energy output balances out the heater input energy. IF the heater is turned off, then the temperature of the interior will drop, as will the surface temperature, until it reaches its previous temperature that existed before the heater was turned on.

Your specific question is not relevant, unless the box is in a vacuum and completely isolated from thermal conduction. Only then will the thermal absorptance match the thermal emittance. This does not mean that the thermal absorptivity equals the thermal emissivity, as there may be spectral differences due to the fact that the sky temperature is substantially colder than the box, so their peak emmissive wavelengths as calculated by Wien's Displacement Law would be drastically different.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
I had a related (?) thread awhile back way back in 2004. I'm not sure about the answer.
thread250-107302

=====================================
(2B)+(2B)' ?
 
Upvote 0 Downvote
That's basically Kirchoff's Circuit Law, which essentially states that what goes into a node (black box or whatever) must come back out, i.e., the algebraic summation of dynamic quantities must be zero. Now, a black box could have something like a phase change material that can temporarily suck up incoming energy, until it has no more capacity to change phase, at which point thermal equilibrium is achieved, and the previous discussions hold sway. Note that the heat capacity acts in a similar fashion, i.e., the temperature change of a black box typically lags the energy input, since the heat capacity equation needs to be satisfied; but, like phase-change, the heat capacity is not infinite, so at some point in time the temperature again achieves equilibrium.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Kirchoff's "Law" is completely accurate - but it is derived from many simplifications and approximations that make it impractical for the real world.

Here, even the original poster simplifies his question back by claiming totally black night, but doesn't specify radiation angles from the "surroundings" (box on a telephone pole in the desert?, box in a room underground?, box in wood barn on dirt?, box in a ship's tank with dirty metal and oil-covered walls all around?), emissivity of the box and surrounding landscape, atmosphere temperature, wind speed, relative humidity, clear or cloudy skies, openings in the "black box" (grey box), internal heat created etc.

Provide some real world information please. Heat transfer is 10% theory combined with 40% measured coefficients and approximations, added to 50% simplifications and additional real world approximations. Even then, you get +/- 10% to 5%.
 
Upvote 0 Downvote
OK,
The box sits high in the air at atmospheric pressure and everything in its surroundings is at temperature T[sub]a[/sub]. The surface (top) facing the sky sees sky radiation and the other five surfaces see radiation from the environment. My question is: how can I say that the total hemispherical IR absorptance of the (finished or unfinished) metal surfaces is equal to the total hemispherical IR emittance of those surfaces?

ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Upvote 0 Downvote
You can say it if the temperature is not changing; it's just conservation of energy:
continuity_otmuty.gif


So if internal power is zero, and there is no convection, then the absorbed power equals the emitted power.


TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Kirchhoff's law of thermal radiation states that absorptivity α is equal to emissivity ε for a given wavelength λ (and to be strictly correct, for a given angle of incidence). This is widely misinterpreted, so it is very important to understand this in detail.

Absorptivity is the fraction of radiation at that wavelength that is absorbed. Emissivity is the fraction of the theoretical maximum thermal radiation (i.e. the "blackbody" radiation) at a given temperature that the body emits.

So if a body absorbs 90% of 15-micron radiation that strikes it, it will emit 90% of what an ideal blackbody would emit at 15-microns at any given temperature.

What it does NOT state is that the intensity of radiation emitted at a given wavelength is equal to the intensity of radiation absorbed at that wavelength. (This is a very common misconception.) So absorptance does not necessarily equal emittance, even for a given wavelength.

As noted, emissivity/absorptivity can vary with wavelength, so you must be very careful in the general case integrating over wavelengths.

However, for a wide variety of materials, the absorptivity/emissivity over the wavelengths of "thermal infrared" radiation relevant for earth ambient temperatures is nearly constant (often ~0.95), so the graybody approximation works well, meaning that you can get good answers without formal integration, and using α=ε overall. Unpainted polished metals are a significant exception to this generalization.

As to a particular example, an upward facing high-emissivity graybody surface at night is likely to emit more thermal IR than it absorbs, particularly on a clear night. One of my heat transfer profs told us to use as a rule of thumb that a clear night sky radiated downward as if it were at blackbody at about -20C (253K).

Such a surface will reach steady-state temperature below the air temperature immediately above it, with the incoming downward radiation plus the conduction from the warmer air balancing the larger emitted upward radiation. This is why you can get frost on these surfaces even when the air temperature stays several degrees above 0C.
 
Upvote 0 Downvote
cswilson said:
However, for a wide variety of materials, the absorptivity/emissivity over the wavelengths of "thermal infrared" radiation relevant for earth ambient temperatures is nearly constant (often ~0.95), so the graybody approximation works well, meaning that you can get good answers without formal integration, and using α=ε overall. Unpainted polished metals are a significant exception to this generalization.
Click to expand...

I have read that organic commercial finishes are decidedly "non-gray" and that many people fall into the trap of assuming they are gray. Are you saying that, although it's true that organic commercial finishes are generally non-gray, over the thermal IR spectrum (only) they are gray? Where can I find it written that "for a wide variety of materials, the absorptivity/emissivity over the wavelengths of 'thermal infrared' radiation relevant for earth ambient temperatures is nearly constant (often ~0.95), so the graybody approximation works well..."

ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Upvote 0 Downvote
There are lots of sources for tables of infrared emissivities, both online and in paper. Here's one it took me less than a minute to find.

Infrared_Emissivity_of_common_materials_uunnlr.jpg


When the overall emissivity is above 0.9, as with many entries in this table, it MUST be at least very close to a graybody, because the emissivity at any individual wavelength cannot be above 1.0.

Now, I cannot say what the infrared emissivity of your particular coating is. Even if the emissivity is significantly below 1.0, I believe that most people still treat it as a graybody, just with a lower ε, as a good enough approximation.

If you can't get good information from a supplier, you still should be able to get a reasonable value easily with a simple experiment. A kitchen infrared thermometer typically assumes an emissivity of 0.95 (that for water). I would first confirm that you get close to 100C reading on boiling water.

Then heat up your coated object substantially above ambient (so you are not fooled by reflected ambient IR), and compare what the IR thermometer says compared to what a contact thermometer says. You should be able to back out the emissivity from the difference.
 
Upvote 0 Downvote
cswilson thank you for finding a big table of emittances for many materials. I have many in my files but could you provide a link to that one? I don't have so many for non-metals.

I know of the ASTM methods for measuring the total hemispherical IR emittance of various surfaces. Most of your post was "preaching to the choir". But I am writing a paper where I must PROVE (with a source of high credibility) that the total hemispherical IR emittance is equal to the total hemispherical IR absorptance over the range of wavelengths for thermal radiation. I don't think I could cite guys on eng-tips.com, January 15, 2019.


ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Upvote 0 Downvote
I found that table simply by searching on "infrared emissivity table". (I used Bing.) Unfortunately, that one does not have a traceable source.

It is easy to find others. For example, here is one from Lawrence Berkeley Labs' website:


As to "proving" that "the total hemispherical IR emittance is equal to the total hemispherical IR absorptance over the range of wavelengths for thermal radiation", I'm not sure what the best approach here is.

First, I am assuming that that sentence uses "emittance" and "absorptance" to mean the same thing as I mean by "emissivity" and "absorptivity".

If that is right, it is just a case of properly citing Kirchhoff's Law of Thermal Radiation, which states that ε(λ,θ) = α(λ,θ) for all wavelengths and angles. Since this is true for every individual wavelength and angle, it must be true for the integrated total. This is true whether it is a blackbody, graybody, approximate graybody, or not even close.

It might be simply a question of citing an authoritative textbook. One I've been using lately is that of MIT professor John Lienhard. It's available free on-line:


Page 533 discusses Kirchhoff's Law, and more rigorously than I have done.

You might also search for any papers that try to "validate" the law experimentally.

(
 
Upvote 0 Downvote
Thanks for that!
OK, I have Leinhard's book but for some reason, my page 533 is different than yours. I've included a screen capture showing the most relevant part. His book warns that the equation ε=α is only used in very specific circumstances and that ε [sub]λ[/sub] (T,θ,Φ)=α[sub]λ[/sub] (T,θ,Φ) is the more general one. I wonder if that last equation could better be written ε(λ,T,θ,Φ)=α(λ,T,θ,Φ).

Capture_ktohld.jpg


I'm thinking that no authors are willing to "stick their necks out" to say anything more specific than that. I'm looking for someone willing to say that, for typical terrestrial temperatures with "smooth" organically-finished surfaces within the thermal infrared range 3μm ≤ λ ≤ 100μm, ε=α holds true.

As for the use of the "tance" and "ivity" suffixes for surface radiation properties, on one hand, NIST says that "ivitiy" suffixes should be used only for "optically pure" surfaces but on the other, their scientists and engineers use the suffixes interchangeably.

ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Upvote 0 Downvote
emittance refers to the radiometric emission, the actual radiance
emissivity is the coefficient you multiply Planck's equation by to get the correct spectral radiance.

I still don't get what you are trying to do. While the relationship holds true if the wavelengths of the absorbed and emitted radiation are exactly equal, they rarely are. In your example above, the sky temperature can be as cold as 220 K, while the surface temperature might be a balmy 270 K; that temperature difference puts the peaks of the blackbody radiation at 13.2 um and 10.7 um, respectively. Moreover, the atmosphere is not completely transparent, so even if you had an perfect gray body, the atmosphere would likely muck things up.

The end result that I think you should care about is P[sub]in[/sub] = P[sub]out[/sub] and that there exists an equilibrium temperature at which the relationship is true.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
IRStuff I beg to differ with you. NIST scientists see no difference between radiation properties called with "tance" or "ivity" as they use them interchangeably. But NIST's official position is the "ivity" is only for what they call "optically pure" surfaces. Of course, they didn't define "optically pure" so it sounds like the use of "tance" is only their preference.

Now you keep mentioning an energy balance but the energy balance involves convection terms as well. It's not a pure radiation problem.

ElectroMechanical Product Development
(Electronics Packaging)
UMD 1984
UCF 1993
 
Upvote 0 Downvote
Total energy in = total energy out, by whatever means or combination thereof. If there is convection or conduction, then the radiative transfer in will definitely not equal the radiative transfer out.

Regardless of what someone at NIST might be confused about does not mean that we should. It's pretty clear that some people understand that spectral emissivity is the ratio of actual emittance divided by the ideal blackbody emittance. Emissivity is unitless; emittance is not.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert! faq731-376 forum1529 Entire Forum list
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

CRisReD
  • Locked
  • Question
Design of Heat Electric Radiation Oven for Electrostatic Powder Paint Curing 1
Replies
13
Views
14
SwinnyGG
SwinnyGG
Uralsk
  • Locked
  • Question
Black colored anodized Aluminium coated bimetallic solar powered distillation equipment?
Replies
3
Views
8
davefitz
davefitz
gahhhrrrlic
  • Locked
  • Question
Radiation view factor confusion
Replies
11
Views
12
georgeverghese
georgeverghese
WelshEngineer87
  • Locked
  • Question
Thermal Radiation Questions
Replies
4
Views
5
goutam_freelance
goutam_freelance
HishamTB
  • Locked
  • Question
Environmental Control Question
Replies
0
Views
1
HishamTB
HishamTB
Back
Top