Extremely basic question about compressible flow 9

[SilverRule]

Hi Guys,

I've searched the forum and haven't found this exact question asked which is very basic and fundamental.

In incompressible flow, I know that static pressure energy is converted to heat (or vibration/noise) exclusively because kinetic energy (velocity) must be constant in this type of flow due to law of continuity.

But in compressible flow, is it true that static pressure energy is not exclusively converted to heat because the pressure drop in this case is converted to increase in volume and therefore shows up as increase in kinetic energy (velocity) for the most part and only some of it is converted to heat?

Is that right?

What determines how much is converted to volume/KE/velocity increase and how much is converted to heat?

Please let me know if any of my premises is wrong.

Following up on the above...

1) Is Compressible Isothermal flow (P1V1 = P2V2) a case where all of the static pressure energy (decrease in pressure) is converted to KE (increase in volume) and none of it is converted to heat?
2) Is Compressible Adiabatic flow a case where only some of it is converted to KE and the rest of it is converted to heat and shows up as rise in temperature?

Thank you!

SR

 

[katmar]

My reply of July 17 does not contradict my earlier posts, but I did not restate the underlying assumptions so it may appear to be contradictory. Your question was "why is it that isothermal flow gives a bigger pressure drop for a certain flow?" and my comments were based on the assumptions implicit in that question.

Let me try again. Under the assumption of the same mass flow rate, with the same compressible fluid and the same pipe dimensions the isothermal model will predict a higher rate of expansion for the gas than the adiabatic model would. The reason for this is the temperature behavior I explained earlier. This higher rate of expansion leads to higher velocities and therefore higher pressure drops for the isothermal model.

Conversely, under assumptions of the same pressure drop the isothermal model will predict lower mass flow rates.

Katmar Software - AioFlo Pipe Hydraulics

http://katmarsoftware.com

"An undefined problem has an infinite number of solutions"

 

[SilverRule]

Latexman/katmar,

Ah! My fault guys.. I overlooked that detail. Thanks for being patient with me. Now there's no confusion on that end. I now understand these macro patterns.

I tend to try to understand all the fundamental underlying theory, so I was studying the wikipedia page on Joule-Thomson expansion effect closely in detail, because as I understand it, that is essentially the fundamental expansion that we see in compressible flow, which we've been discussing in this thread (yes, I understand that gas flowing in insulated pipe isn't as clean of an example of this effect as flowing across a throttled valve as this flowing in uninsulated pipe isn't quite adiabatic/isenthalpic but the effect is still in play at a milder level). I was confused by something in this section of the wiki page ->

https://en.wikipedia.org/wiki/Joule–Thomson_effect#Physical_mechanism

"In a Joule–Thomson expansion the enthalpy remains constant. The enthalpy, H, is defined as H = U + PV where U is internal energy, P is pressure, and V is volume. Under the conditions of a Joule–Thomson expansion, the change in PV represents the work done by the fluid. If PV increases, with H constant, then U must decrease as a result of the fluid doing work on its surroundings. This produces a decrease in temperature and results in a positive Joule–Thomson coefficient. Conversely, a decrease in PV means that work is done on the fluid and the internal energy increases. If the increase in kinetic energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule–Thomson coefficient will be negative."

That PV increase being referred to in bold.. this is how I'm interpreting it (please correct me if this is wrong): If P1 and V1 are 100 and 75, respectively, and P2 at some downstream location is 50, then V2 will have to be higher than 150... in which case, PV has increased due to the PV expansion work having done by the system. If PV is said to be constant in isothermal flow, meaning it could only expand up to 150, how could the PV increase in adiabatic flow? Shouldn't there be smaller expansion in adiabatic flow? So I would expect PV to decrease instead.

Any idea what I'm misunderstanding here? I'm almost sure I'm comparing to apples to oranges here again but can't pick out what exactly.

Sorry if this is a bit too esoteric/theoretical. You guys have been very helpful so far.

 

[Latexman]

Apples and oranges again. How can you use an isothermal behavior (PV¹ = constant) to question adiabatic behavior (PV^k = constant)?

Good Luck,
Latexman
Pats' Pub's Proprietor

 

[SilverRule]

Apples and oranges again. How can you use an isothermal behavior (PV1 = constant) to question adiabatic behavior (PVk = constant)?

Oh no.. I'm not asking this question -> "Since PV must be constant for isothermal flow, how is it that they're saying PV increases in adiabatic flow?" That would be definitely be an absurd question blatantly trying to compare apples to oranges.

It's more like this -> "We recognize that PV = constant for isothermal behavior. And we recognize that PV^k = constant for adiabatic behavior. So for adiabatic behavior, if PV^k = constant, then it would be correct to say that PV itself decreases for adiabatic ... in other words V2 wouldn't be as high as it would have been in the isothermal case. So based on this assumption, I'm questioning why that wiki page says that PV increases, rather than decrease, suggesting that V2 would actually be higher than it would have been in the isothermal case."

Hope my question is clear now

 

[Latexman]

This diagram of expansion processes may help. Or, work out a real example using PV^k = constant and PV = constant on a graph, but don't go past the critical pressure ratio like on the previous example.

Good Luck,
Latexman
Pats' Pub's Proprietor

 

[SilverRule]

Yes, that diagram or even a worked example using simple numbers would illustrate that the value of PV (i.e. P multplied by V) would decrease for adiabatic process. The volume doesn't increase sufficiently enough to keep PV constant (like it does in isothermal case). So P2*V2 would be less than P1*V1. So with that being the case, how come wikipedia says (in bold in my earlier post) that PV increases?

 

[Latexman]

It's wrong and needs fixing? It seems the current focus is on what makes the JT coefficient positive or negative,

Good Luck,
Latexman
Pats' Pub's Proprietor

 

[SilverRule]

It's wrong and needs fixing? It seems the current focus is on what makes the JT coefficient positive or negative,

Well no, I'm not saying wiki got it wrong and needs fixing necessarily (unless you're saying that) ... I don't know if it's right or wrong, I'm just seeing a dissonance between what you and katmar have said (volume not increasing sufficiently enough to keep PV constant for adiabatic) and what wiki is saying about PV increasing when there's a cooling. The logic in wiki seems to make a lot of sense when you look at the equation H=U+PV ... because temperature is captured within U, when it goes down, PV needs to go up in order to keep H constant (to adhere to the isenthalpic requirement).

I'm just not sure why there seems to be a dissonance. Do you think the wiki has it wrong?

The current focus is not really on what makes JT coefficient positive or negative, it's just that wiki's explanation of how the value of PV changes is nested inside its explanation of what makes JT coefficient positive or negative. We're really only interested in the cooling case (positive JT coefficient) where it says PV increases as this is the most common case you're dealing with.

 

[Latexman]

I wasn't sure they were wrong either, that's why I had the ? mark.

If PV increases, with H constant, then U must decrease as a result of the fluid doing work on its surroundings.

The IF, in front makes me think they are talking hypothetically and not about a specific case. This is supported further down before their "proof" with the discussion on a gas changing sign of the JT coefficient before/after it's inversion point:

They are covering all the cases, not just the usual expansion with a drop in temperature we see in compressible flow of most gases and vapors. I think from that respect what they say is correct.

Good Luck,
Latexman
Pats' Pub's Proprietor

 

[SilverRule]

Sure I'm willing to assume they're trying to cover all cases. But the thing is, I don't even see where they cover the usual case of temp dropping AND PV decreasing anywhere. The only time they talk about PV decreasing is here:

"Conversely, a decrease in PV means that work is done on the fluid and the internal energy increases. If the increase in kinetic energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule–Thomson coefficient will be negative."

This doesn't seem to be the usual case because in the usual case the fluid would be doing the work (rather than not getting work done on) and thermal kinetic energy (temp) decreases rather than increase.

Something is not adding up here on a semantic level..

Let me ask you this in case we've got the semantics flipped: When a fluid is doing (expansion) work as opposed to getting work done on, would the PV value in H=U+PV increase or decrease? And during the usual expansion in compressible flow, is the fluid doing the work or getting work done on?

 

[TiCl4]

Is anyone else amused that the thread with “extremely basic” in the title has garnered so much attention, thought, and deliberation? Apparently basic questions do not always beget simple answers!

 

[Latexman]

I've found over time some compressible flow threads take a life of their own. It's a fascinating subject that is commonly used by almost every discipline.

Good Luck,
Latexman
Pats' Pub's Proprietor

 

[SilverRule]

Yeah, that struck me too as interesting. I think it reaffirms the saying "You don't know what you don't know". Initially I thought it was rather straightforward but the more we got into it, new questions that I hadn't considered kept popping up.

But the gentlemen here have done an awesome job clearing everything up and I really believe this is the last outstanding unanswered question in this "thread" so to speak. I find it hard to believe that either wikipedia or the guys here are wrong, so I'm trying to find the missing piece that would reconcile the two.

 

[SilverRule]

If anyone would like, let me just restate the question at hand:

I was studying the wikipedia page on Joule-Thomson expansion effect closely in detail, because as I understand it, that is essentially the fundamental expansion that we see in compressible flow, which we've been discussing in this thread (yes, I understand that gas flowing in insulated pipe isn't as clean of an example of this effect as flowing across a throttled valve as this flowing in uninsulated pipe isn't quite adiabatic/isenthalpic but the effect is still in play at a milder level). I was confused by something in this section of the wiki page ->

https://en.wikipedia.org/wiki/Joule–Thomson_effect#Physical_mechanism

"In a Joule–Thomson expansion the enthalpy remains constant. The enthalpy, H, is defined as H = U + PV where U is internal energy, P is pressure, and V is volume. Under the conditions of a Joule–Thomson expansion, the change in PV represents the work done by the fluid. If PV increases, with H constant, then U must decrease as a result of the fluid doing work on its surroundings. This produces a decrease in temperature and results in a positive Joule–Thomson coefficient. Conversely, a decrease in PV means that work is done on the fluid and the internal energy increases. If the increase in kinetic energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule–Thomson coefficient will be negative."

That PV increase being referred to in bold.. this is how I'm interpreting it (please correct me if this is wrong): If P1 and V1 are 100 and 75, respectively, and P2 at some downstream location is 50, then V2 will have to be higher than 150...which represents the PV increase.

BUT if PV = constant in isothermal flow meaning it could only expand up to 150 (V2 = 150), and if PV^k = constant for adiabatic flow meaning PV itself would decrease (i.e., P2*V2 < P1*V1) and so V2 wouldn't be as high as it's in the isothermal case...HOW COME the wiki quote says that PV increases suggesting that V2 would actually be higher than it's in the isothermal case? How could the PV increase in adiabatic flow? Shouldn't there be smaller expansion in adiabatic flow? So I would expect PV to decrease instead.

 

[SilverRule]

Can anyone tell me if my question makes sense please? I'm not sure if the question is incomprehensible or if you guys aren't sure of the answer either.

Maybe this thread has gotten too deep and messy and maybe I should just make a new clean independent thread with the question?

Thank you!

 

[Latexman]

Isothermal flow is approached in long pipelines where heat transfer is relatively rapid. Friction is accounted, because it is not negligible to the process. L/d approaches [&infin;].

The Joule-Thomson effect is approached in an insulated valve, so minimal heat is transferred. A valve is extremely short, comparatively. Friction is not accounted, because it is negligible to the process. L/d approaches 1.

Apples and oranges.

Good Luck,
Latexman
Pats' Pub's Proprietor

 

[SilverRule]

First of all, thank you for the response. There's a few separate things that need to be parsed out here...

I'll first lay out all the expansion scenarios. I've got this from a wide mix of sources:

Joule-Thomson (JT) expansion effect is isenthalpic, so H=U+PV must be constant. U consists of thermal KE (temperature) and thermal PE (attractive Van der Waals forces between molecules).

- If a real gas is expanding into a vacuum across a throttle, they call it Free Expansion instead of JT expansion because it's not expanding against a pressure. Since it's not going against a pressure, it doesn't have to do any PV expansion work. But still, as it has attractive molecular forces that need to be overcome for it to expand, the temperature drops and is converted to thermal PE. So overall, PV doesn't change since it's Free Expansion and U doesn't change on a macro level. Just the magnitudes of the constituents of U change. So H is constant overall.

- If an ideal gas is expanding against a pressure, AKA regular flow, across a throttle, this isn't a JT expansion. This is because...since there are no attractive molecular forces to overcome, there is no PV expansion work that needs to be done, and the gas expands without the temperature having to drop. So, PV is constant. Since temperature is constant and thermal PE is constant, U is constant. Overall H is constant.

- If a real gas is expanding against a pressure, AKA regular flow, across a throttle, this is the JT expansion. There are attractive forces to overcome, and since it's going against a pressure, PV expansion work needs to be done to overcome these forces. So here temperature is sacrificed/dropped and converted to do PV expansion work. Here is where wikipedia says PV increases. It doesn't mention if the magnitude of thermal PE also increases. I'm assuming it does since molecules have more separation now. So here, PV changes, and thermal KE and thermal PE that make up U also change. Again, the changes in U and PV would balance each other out to keep H constant.

These are the fundamental mechanisms. I thought laying this out would help understanding of what's below.

Directly to your comment: I also thought initially that the Joule-Thomson (JT) expansion effect only applied to valves only as the heat transfer is negligible in that scenario. But after diving deep, I learned that JT is actually in effect in any conduit that is adiabatic. So if a pipe is perfectly insulated the JT effect is working EXACTLY the same way there throughout the whole pipe. In fact that's not even the full picture...in reality, even in an UN-INSULATED pipe the JT effect is happening...it doesn't have to be adiabatic...only difference is that the effect is milder (you don't see as big a temp change). So adiabatic will show the purest, cleanest and maximal JT effect and non-adiabatic (polytropic) will show a lesser JT effect and isothermal will effectively show none.

I say isothermal will effectively show none because just like polytropic and adiabatic, it will also cool, as it flows over a unit length of pipe. Why will it cool? Because as the pressure drops it has to cool in order to expand -- since this is a real gas going against pressure, there is no expansion possible without JT effect of cooling (as per the mechanism described above). So the reason this is ending up as isothermal effectively is because of the heat transfer which raises the temperature back up. So my point is that JT expansion is not fundamental only to adiabatic flow. It's just that...effectively that is the flow that sees its maximal impact.

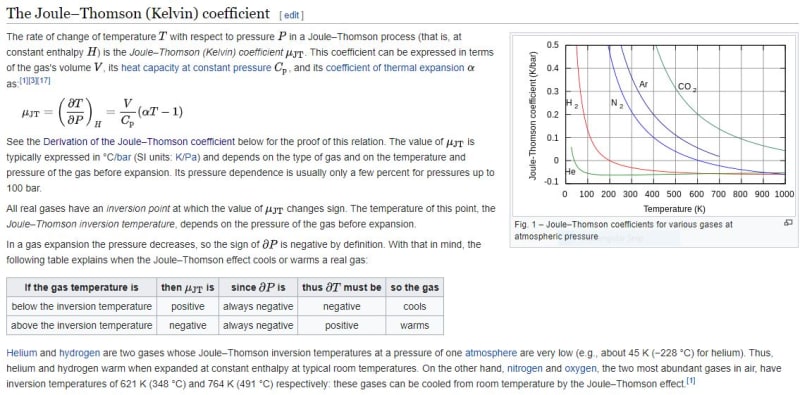
Again, for a real gas, JT expansion is inherently built-in to the entire flow, not just across the valve. There is no flow without JT expansion, whether that cooling is being "reversed" by the heat transfer/input that may also happening at the same time (isothermal) or not (adiabatic). This was a big revelation to me. Hope that makes sense.

The sources that made this particularly explicit/clear to me:

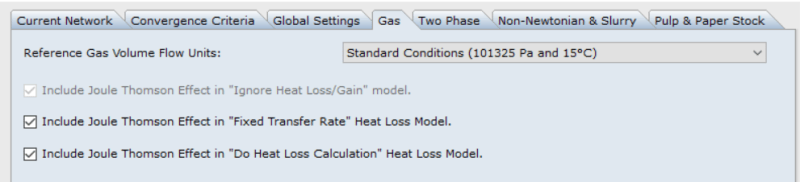
1) My flow simulation program: It automatically does the JT calculation across a valve. And if you select the adiabatic model for the pipe as if it's perfectly insulated, it again automatically includes the JT calculation. It won't even let you uncheck that calculation. If you select a non-adiabatic (heat transfer) model for the pipe, then it lets you check or uncheck the JT calculation. See image below.

2)

https://www.cambridge.org/th/files/1613/6690/0251/9743_Adiabatic_Processes.pdf

Look at the bottom of page 13 in the ISENTHALPIC PV WORK - The Irreversible Case section. It says the following:

"Pippard (1966, pp. 68–72) points out that an isenthalpic expansion need not have a throttle, but could take place for example in a tube in which the entropy-producing effect of the throttle is replaced by viscous drag along the walls, or possibly by other entropy-producing processes such as turbulence, chemical reactions, and so on. In other words, the essential element of a Joule-Thompson expansion is not the presence of a throttle; it can be any adiabatic irreversible change between two equilibrium states having the same enthalpy."


Please let me know if anything I said is confusing or needs any clarification. I would really appreciate it!!

 

[SilverRule]

Hey guys,

Has anyone been able to have a chance to digest my last post?

SR

 

[SilverRule]

Anyone?

 

[SilverRule]

Hey guys,

I think I may have figured out the answer to my own question (possibly) if anyone is interested..

As I expected, I think it's confusion arising from semantics..

I think the PV quantity in the enthalpy equation H=U+PV has a slightly different meaning than the PV in PV^k=constant.

The change in PV in the former context is at the "micro" infinitesimal level strictly as a means of calculating the expansion work which would take the generic form of W=P*DeltaV. So at the micro level, P is basically held constant as the volume changes/increases (recall back to how you manually would integrate the area under a PV curve). So of course PV would increase in that micro expansion causing U to decrease leaving H constant. This is how PV is used here even though the overall quantity of PV decreases at macro level for all practical purposes because P actually decreases in reality instead of holding constant.

This was really bothering me so I feel much better now. I guess my whole confusion came back from completely forgetting the theoretical basics.

If anyone sees anything off with this, let me know.

Thanks a lot to EVERYONE who's responded in this thread. I really appreciate y'alls help!