maatjie_mike
Mechanical
Hi,
I am doing pretty standard bolt calculations and noticed a difference between the power screw and regular fastener calcs. The fastener situation I have is bolts holding a pressurized pipe flange together (ie. external load is in the same direction as the preload (or rather opposite direction but same axis))
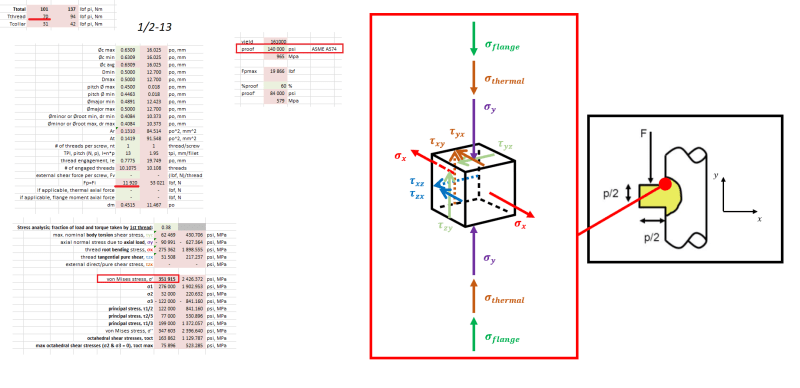
The textbook im using is shigley and a lot of sources on the net but I cannot find a solution to the questions below (please see attached pic for ref):
1) For power screws Von Mises is used to combine axial stress, thread bending and thread shear due to rotation. I know that the thread shear stress due to rotation is zero but why isnt Von Mises used to combine the axial and thread bending for normal fasteners?
2) Why isnt thread shear due to applied force taken into account?
All examples equate the preload force to 75% or 90% of the proof strength (or rather the force that produces the proof strength in the minimum area of the fastener). adding the external force will slightly increase the tensile stress in the bolt but not enough to exceed the proof strength. Now if you combine the tensile stress and the bending stress using Von Mises then the stress in the fastener exceeds the proof strength which means the bolt will yield (fail). when doing power screw calcs this bending stress is taken into account but not when doing normal fastener calcs.
If the reason is the shape of the thread, which approach do I use if using ACME thread for a regular fastener?
Kind regards
Michael Mullineux
I am doing pretty standard bolt calculations and noticed a difference between the power screw and regular fastener calcs. The fastener situation I have is bolts holding a pressurized pipe flange together (ie. external load is in the same direction as the preload (or rather opposite direction but same axis))
The textbook im using is shigley and a lot of sources on the net but I cannot find a solution to the questions below (please see attached pic for ref):
1) For power screws Von Mises is used to combine axial stress, thread bending and thread shear due to rotation. I know that the thread shear stress due to rotation is zero but why isnt Von Mises used to combine the axial and thread bending for normal fasteners?
2) Why isnt thread shear due to applied force taken into account?
All examples equate the preload force to 75% or 90% of the proof strength (or rather the force that produces the proof strength in the minimum area of the fastener). adding the external force will slightly increase the tensile stress in the bolt but not enough to exceed the proof strength. Now if you combine the tensile stress and the bending stress using Von Mises then the stress in the fastener exceeds the proof strength which means the bolt will yield (fail). when doing power screw calcs this bending stress is taken into account but not when doing normal fastener calcs.
If the reason is the shape of the thread, which approach do I use if using ACME thread for a regular fastener?
Kind regards
Michael Mullineux