DrMetal
Materials
- Oct 4, 2005
- 30
GIVEN: X-Y-Z coordinates of 3 points in 3D space. FIND: Radius of circle on those 3 points & Circle center co-ordinatesBookmark:
Question: Can someone provide a mathematical step by step procedure to calculate and determine a circle radius and the center point coordinates from three GIVEN 3D points with X-Y-Z coordinates?
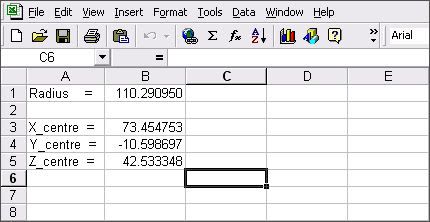
- I have searched the web extensively, and found lots of proposed solutions, but my college math is quite rusty and after several days, I still can not come up with the correct detailed solution. I can do this easily from three points in 2D, in Excel using three simultaneous equations with TWO variables (i.e. find circle center @ h, j). But I can't get it to work in 3D with a similar spreadsheet approach with THREE variables (i.e. find circle center @ h-j-k). Seems I keep going in mathematical circles (no pun intended) with a modified Excel approach with the three quadratic equations.
- Is it possible to solve this mathematically with (3) simultaneous quadratic equations? Or do I need a 4th equation, determinates, etc?. Seems when I try the double elimination (or substitution) of variables approach, I keep coming up with unsolvable, or meaningless equations. With as much time as we have spent on this problem, we would be happy to compensate someone for their time to solve this for us.
- We have several drawings with bent pipes in 3D where we have only THREE 3D points given to us. We need to be able to determine the TRUE bend radius of the pipes. These are special alloy pipes @ $25k each, so we want to be sure we have the correct 2D bend radius before we bend them. I'd prefer an approach that could be put into a spreadsheet to make reiterative calcs go quickly. I'd prefer to have a detailed step-by-step solution vs. being directed to one of the web solutions. I have seen most of them, and still am stuck on this.
Thanks, MWP
Question: Can someone provide a mathematical step by step procedure to calculate and determine a circle radius and the center point coordinates from three GIVEN 3D points with X-Y-Z coordinates?
- I have searched the web extensively, and found lots of proposed solutions, but my college math is quite rusty and after several days, I still can not come up with the correct detailed solution. I can do this easily from three points in 2D, in Excel using three simultaneous equations with TWO variables (i.e. find circle center @ h, j). But I can't get it to work in 3D with a similar spreadsheet approach with THREE variables (i.e. find circle center @ h-j-k). Seems I keep going in mathematical circles (no pun intended) with a modified Excel approach with the three quadratic equations.
- Is it possible to solve this mathematically with (3) simultaneous quadratic equations? Or do I need a 4th equation, determinates, etc?. Seems when I try the double elimination (or substitution) of variables approach, I keep coming up with unsolvable, or meaningless equations. With as much time as we have spent on this problem, we would be happy to compensate someone for their time to solve this for us.
- We have several drawings with bent pipes in 3D where we have only THREE 3D points given to us. We need to be able to determine the TRUE bend radius of the pipes. These are special alloy pipes @ $25k each, so we want to be sure we have the correct 2D bend radius before we bend them. I'd prefer an approach that could be put into a spreadsheet to make reiterative calcs go quickly. I'd prefer to have a detailed step-by-step solution vs. being directed to one of the web solutions. I have seen most of them, and still am stuck on this.
Thanks, MWP