Jake-Designer
Mechanical
- Feb 25, 2017
- 5
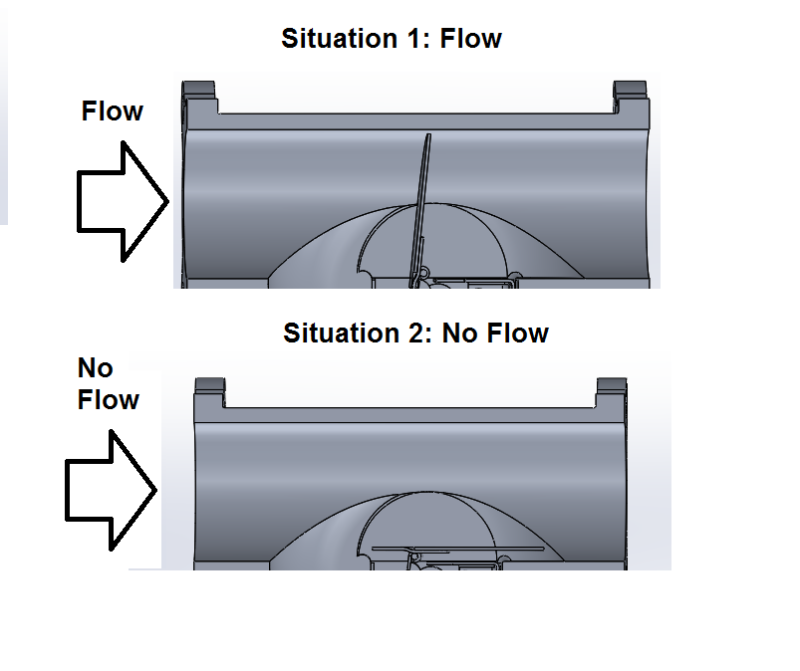
I am working on a design problem where I have a pipe filled with water. Within a pipe there is a gate connected to a hinge. I am trying to gain a better understanding of two situations. The first situation is when a boost pump moves the fluid what is the force against the gate, I believe I can model with dynamic pressure where F = q * Area and q = (1/2) * density * velocity * velocity. The second situation is if the boost pump is turned off, stopping the flow of fluid and I apply a moment to the hinge what factors do I need to consider for returning it back to the upright position.
I have read through some online resources and some fluid mechanics textbooks that I have but haven't been able to find a concrete example of what I am doing. Any good references would be greatly appreciated.
Thanks!
I have read through some online resources and some fluid mechanics textbooks that I have but haven't been able to find a concrete example of what I am doing. Any good references would be greatly appreciated.
Thanks!