I'm trying to figure out the force required to lift up one end of a long pipe by 2m. The pipe is long enough that the entire length of it will not lift off the ground. It will bend under it's own weight and become tangent with the ground at some unknown point away from the end.
I tried to model this using various beam formulas but I end up with two unknowns (the force on one end and the length that lifts off) and can't solve them.
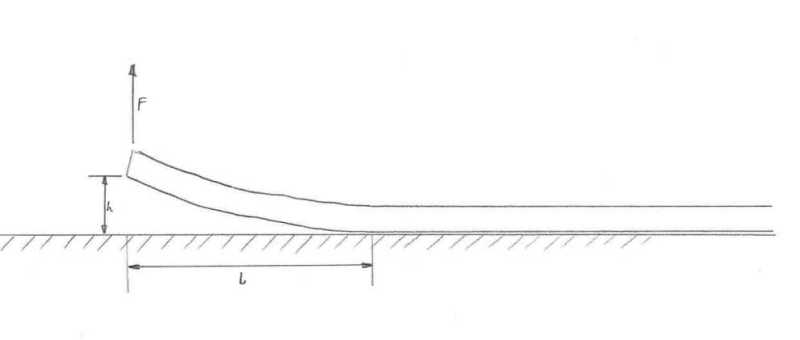
I tried to model this using various beam formulas but I end up with two unknowns (the force on one end and the length that lifts off) and can't solve them.

