Formula for warping constant of box section 3

[EK1989]

Hi,

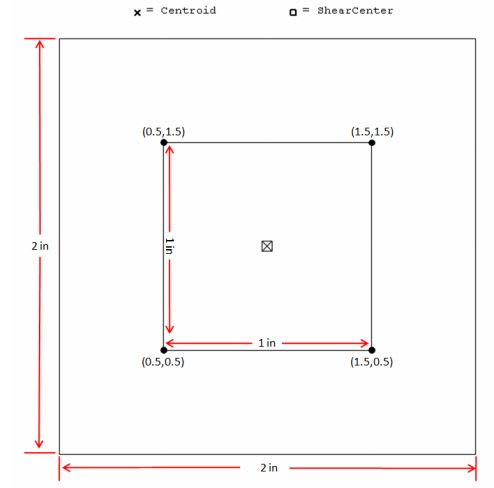
I am trying to verify the section properties that my software provides me for the warping constant but I can not find out how the warping constant is calculated. I have a box section with width and height 2 in and thickness 0.5 in. The warping constant that the software gives me is equal to 0.00730 in^6. Does anyone know if there is an explicit formula to calculate the warping constant of a box section? Although, the warping effects may be negligible in these sections, I would like to check it with some hand calculations.

Thank you in advance!

Kind regards,
Emmanouil

 

[Agent666]

Yes, warping constant = 0 for a closed section. There can be no warping if you think about it, how do you get the deformation compatibility in a closed shape if warping were to occur, it needs to be an open section for the warping deformation to occur.

Most codes state to simply take the warping constant as zero for a hollow section for this reason.

 

[Agent666]

For what its worth, if I put your section through section-properties, I get exactly the same answer as your 0.00730 in^6. Which is pretty close to zero you have to admit.

 

[BAretired]

0.00730 in^6 = 1,960,311 mm^6 which is not too close to zero.

The warping constant for closed sections is normally taken as zero when the walls are thin such as Hollow Structural Sections. I don't know whether or not this applies to rectangular bars or shafts. The section shown in the OP is closed but the walls are not thin relative to the overall dimensions. It may be that it behaves more like a 2" x 2" solid shaft than a hollow section.

For a solid shaft of rectangular cross section, Timoshenko and McCullough in "Elements of Strength of Materials" claim (without proof) that the angle of twist per unit of length θ is given by

θ = M[sub]t[/sub]/βbc[sup]3[/sup]G where b is the longer and c is the shorter side.​

For a solid square shaft, as is the case here, θ = M[sub]t[/sub]/βb[sup]4[/sup]G

The value of β varies with the ratio b/c.
When b/c = 1, β = 0.141 whereas for b/c = 10, β = 0.313 and for b/c = ∞, β = 1/3

I cannot find any reference for a square hollow section with thick walls.

BA

 

[Agent666]

0.00730 in^6 = 1,960,311 mm^6 which is not too close to zero.

Indeed, primarily work in metric, failed to engage imperial brain!

 

[Settingsun]

We're talking 2-3% of the smallest channel's parameter (75mm, 3"), right? I'd say that qualifies as close enough to zero.

 

[Agent666]

I guess whether its significant or not really has to do with the problem being considered, and also how large the warping torsion it is in relation to the torsion constant.

Both 'flexural torsional buckling', and 'torsion' problems feature warping and torsion constants. For example the following is a plot of both the warping constant (Iw or Cw) and torsion constant (J) relative to wall thickness for a 2" x 2" hollow section with square corners (both in mm units).

As you will note, depending on the thickness the relative values of each parameter can be quite a different magnitude when compared directly to the other (hence warping torsion may be more significant than St Venant torsion, and vice versa depending on the thickness). Hence warping constant even if small may prove more significant in whatever engineering problem is being looked into?

 

[Settingsun]

Ok but if I've done my sums right, the contributions of J and Iw to flexural torsional buckling resistance are equal at Le=7.2mm (for 12.7mm walls per original post). Then Iw contribution decreases at Le^2 while J is unaffected by Le. Possibly not entirely accurate at spans less than section dimensions but illustrative nonetheless.

I didn't check this too carefully as it matches my pre-conceived notion. I assume the story of twist deflection is similar.

 

[BAretired]

Agent666,
Cw (or Iw) has units of mm[sup]6[/sup] whereas J has units of mm[sup]4[/sup]. The scale on the ordinate is for Cw. Is there a different scale for J?



BA

 

[BAretired]

steveh49,
Flexural torsional buckling resistance is one issue, but pure torsion is another which may be of interest to the OP. In either case, the warping constant plays a role in the solution. The OP was looking for a formula to calculate Warping Constant.

BA

 

[Settingsun]

I understand he wants a formula and I did try to find one in some books and papers I have. I was quite surprised my Trahair books/papers didn't even mention it - he gets quite theoretical. I suspect the software documentation would be the place to look. I also suspect it isn't simple...

 

[FEA way]

It's hard to find the formula for warping constant of such profile since it's usually used for thin-walled open sections.

I've found this:

It's for more general case of rectangular pipe but should be useful for you too.

 

[EK1989]

Hi,

Thank you all for your replies and your comments. These are very helpful to me.

@Agent666: I downloaded the python code you suggested. Could you forward me the input file you used to compute the warping constant as 0.00730 in^6 for the section that I have.

@FEA way: Thank you for the formula but if I substitute my section parameters there, it gives me Cw=0, while the warping constant is equal to 0.00730. Could you tell me the book/paper you extract that relation, please?

I am looking for an analytical expression of the warping constant for box sections. Indeed, it is very hard to find and I am wondering if there is an analytical solution or it can only be calculated numerically.

Thanks,
Emmanouil

 

[Ingenuity]

Interestingly, the AISC Manual states the property as C (not C[sub]w[/sub]) and is defined as the "HSS torsional constant" with units of in[sup]3[/sup] (or mm[sup]3[/sup]) - not to exponent 6 - presumably because this is for thin-walled members.

 

[Settingsun]

Ingenuity, this might be the parameter for converting from torsion moment to torsion stress. Similar to the elastic section modulus for bending. Hard to say because everyone uses different symbols.

 

[Agent666]

BAretired, just plotting the raw value, units differ between Iw & J obviously, was intending primarily to show how the relationship between the two might differ at various wall thicknesses. (I did note after I posted the plot that I didn't update the title when I added J to the plot for comparison)

Ingenuity, steveh49 is correct, C is the torsion modulus constant. Its analogous to the section modulus for determining flexural strength, but for torsion.

 

[IDS]

A few comments:
The "Make Beam Section" function in the Strand7 FEA package gives the same results as Robbie van Leeuwen's Section Properties program (see Agent 666's second post).
I presume other FEA software will do the same.

I have an Excel front-end to Robbie's Python software that can be downloaded from:
Section Properties with MeshPY, including torsion and warping
It isn't working on my current setup, but for anyone with 32 bit Python2 and xlwings installed it might be worth trying. Otherwise probably better to use the Python code direct.
I will be updating my code when I have time, but that may not be soon.

The formula given by FEAway will evaluate to zero if h=b and t1 = t2; i.e. for any section symmetrical about both principal axes. This is an approximation.
Any axi-symmetric section will have exactly zero warping, but a square section will have small warping strains, as shown by the FEA results.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Agent666]

EK1989, see attached, just copy/paste into a *.py script and run it.

import sectionproperties.pre.sections as sections
from sectionproperties.analysis.cross_section import CrossSection

geometry = sections.Rhs(d=2 * 25.4, b=2 * 25.4, t=25.4 / 2, r_out=0, n_r=1)

geometry.clean_geometry()

mesh = geometry.create_mesh(mesh_sizes=[0.25])

section = CrossSection(geometry, mesh)
section.plot_mesh()
section.display_mesh_info()
section.calculate_geometric_properties(time_info=True)
section.calculate_plastic_properties(time_info=True)
section.calculate_warping_properties(time_info=True)
section.display_results(fmt='.3f')

This should output the following properties:-

Section Properties:
A        = 1935.480
Qx       = 49161.192
Qy       = 49161.192
cx       = 25.400
cy       = 25.400
Ixx_g    = 1768983.559
Iyy_g    = 1768983.559
Ixy_g    = 1248694.277
Ixx_c    = 520289.282
Iyy_c    = 520289.282
Ixy_c    = 0.000
Zxx+     = 20483.830
Zxx-     = 20483.830
Zyy+     = 20483.830
Zyy-     = 20483.830
rx       = 16.396
ry       = 16.396
phi      = 0.000
I11_c    = 520289.282
I22_c    = 520289.282
Z11+     = 20483.830
Z11-     = 20483.830
Z22+     = 20483.830
Z22-     = 20483.830
r11      = 16.396
r22      = 16.396
J        = 860072.306
Iw       = 1961654.050
x_se     = 25.400
y_se     = 25.400
x_st     = 25.400
y_st     = 25.400
x1_se    = 0.000
y2_se    = -0.000
A_sx     = 1053.226
A_sy     = 1053.226
A_s11    = 1053.226
A_s22    = 1053.226
betax+   = -0.001
betax-   = 0.001
betay+   = 0.000
betay-   = -0.000
beta11+  = -0.001
beta11-  = 0.001
beta22+  = 0.000
beta22-  = -0.000
x_pc     = 25.400
y_pc     = 25.400
Sxx      = 28677.362
Syy      = 28677.362
SF_xx+   = 1.400
SF_xx-   = 1.400
SF_yy+   = 1.400
SF_yy-   = 1.400
x11_pc   = 25.400
y22_pc   = 25.400
S11      = 28677.362
S22      = 28677.362
SF_11+   = 1.400
SF_11-   = 1.400
SF_22+   = 1.400
SF_22-   = 1.400

You can check what they all mean on the section-properties readthedocs page. Some of the nomenclature for things like plastic and elastic moduli are the opposite way round for any north american folks, Z is S, S is Z etc, as its based on how it is in the NZ and Australian codes.

EDIT - Note all output in mm units

 

[FEA way]

@EK1989 I found this formula in presentation about thin-walled structures available in the internet (it's in Polish so there's no purpose to share the link). It's clearly a scanned table taken from some book, likely one of the metal structure design guides mentioned in bibliography. I will try to find these books to confirm the source of this equation.

 

[BAretired]

Using the expression by FEA way, Cw = 0, so that doesn't agree with values posted by Agent666 but does agree with the usual assumption for a square HSS.

The output from Python Code for Cw or Iw = 1961654.050 which agrees with earlier values posted. The only problem is that none of us know how it was calculated.

BA