Hi,
I'm simulating a fully coupled thermal-stress problem with linear elastic material in Abaqus/Standard and comparing the results with my own implementation of the same problem in FEniCSx. The weak form in FEniCSx has been derived using the balance equations mentioned in the paper Farhat et al. (1991) Link, which are:
(Screenshot of the paper)
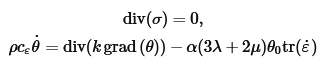
where
σ=2με+λtr(ε)I−α(3λ+2μ)(θ−θ0)I and ε=1/2(grad(u)+grad(u)T). Details on other parameters are fairly standard and can be found in the paper. My FEniCSx results (both temperature and displacement fields) match to those of Abaqus only after I neglect the strain rate term in the heat conduction equation (α(3λ+2μ)θ0tr(ε_dot)) thereby uncoupling the displacement from temperature change. This is in contradiction the Abaqus' analysis description which states that both fields are fully coupled.
Does anyone know which coupled equations does Abaqus/Standard implement for fully coupled thermal-stress analysis? Especially the heat conduction equation? In the Abaqus theory manual I could only find the uncoupled heat conduction equation (link) but no equations on fully coupled thermal-stress analysis. However there is a description of the fully coupled thermal-stress analysis procedure in the Abaqus user manual (link).
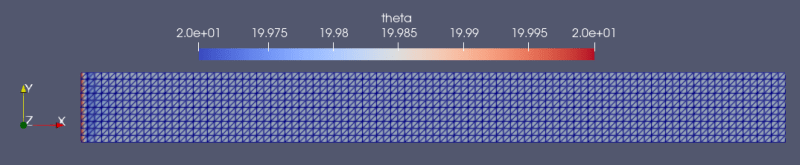
I also tried to model a simple linear thermoelastic 2D-"Beam" fixed at left side and "pulled" using displacement-BC on the right side. The initial temperature was defined as a predefined field (value: 20 in Initial Step and the value is calculated in subsequent step). I am not modelling the beam with plasticity.
See Screenshot on deformed and original state. The time dependent deformation is not resulting in any change in temperature.

Anyone has any idea as to what I'm doing wrong? All relevant material parameters and model constants (Absolute temperature and Stefan-Boltzmann constants) are defined. I have attached the inp file.
Thank you for any leads.
MPa
I'm simulating a fully coupled thermal-stress problem with linear elastic material in Abaqus/Standard and comparing the results with my own implementation of the same problem in FEniCSx. The weak form in FEniCSx has been derived using the balance equations mentioned in the paper Farhat et al. (1991) Link, which are:
(Screenshot of the paper)
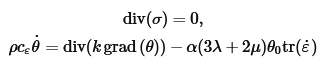
where
σ=2με+λtr(ε)I−α(3λ+2μ)(θ−θ0)I and ε=1/2(grad(u)+grad(u)T). Details on other parameters are fairly standard and can be found in the paper. My FEniCSx results (both temperature and displacement fields) match to those of Abaqus only after I neglect the strain rate term in the heat conduction equation (α(3λ+2μ)θ0tr(ε_dot)) thereby uncoupling the displacement from temperature change. This is in contradiction the Abaqus' analysis description which states that both fields are fully coupled.
Does anyone know which coupled equations does Abaqus/Standard implement for fully coupled thermal-stress analysis? Especially the heat conduction equation? In the Abaqus theory manual I could only find the uncoupled heat conduction equation (link) but no equations on fully coupled thermal-stress analysis. However there is a description of the fully coupled thermal-stress analysis procedure in the Abaqus user manual (link).
I also tried to model a simple linear thermoelastic 2D-"Beam" fixed at left side and "pulled" using displacement-BC on the right side. The initial temperature was defined as a predefined field (value: 20 in Initial Step and the value is calculated in subsequent step). I am not modelling the beam with plasticity.
See Screenshot on deformed and original state. The time dependent deformation is not resulting in any change in temperature.

Anyone has any idea as to what I'm doing wrong? All relevant material parameters and model constants (Absolute temperature and Stefan-Boltzmann constants) are defined. I have attached the inp file.
Thank you for any leads.
MPa