willowman
Civil/Environmental
- Feb 22, 2020
- 25
Hi,
I am new to the graphical static method used to draw funicular polygons but I see that it has tremendous value. I am trying to define the funicular shape of a beam under the action of five parallel point loads.
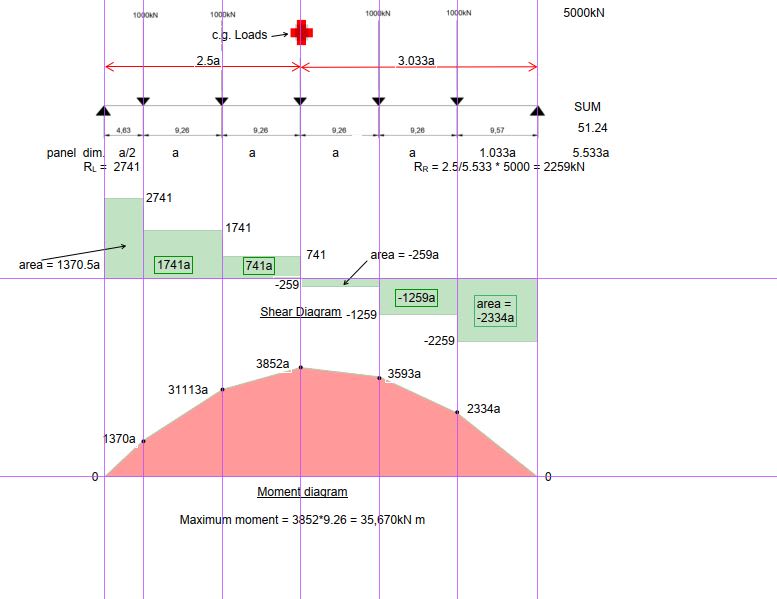
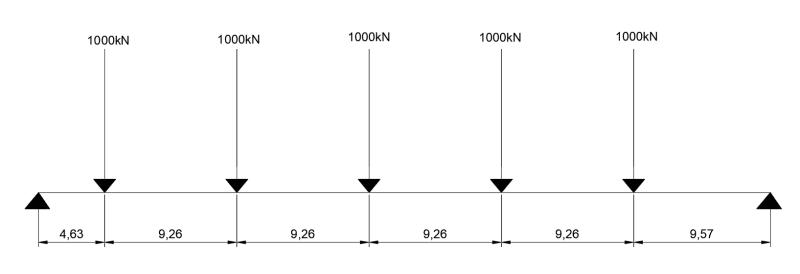
The point loads have equal magnitude but the spacing along the beam varies slightly. Supports at either end of the beam are pinned.
 .
.
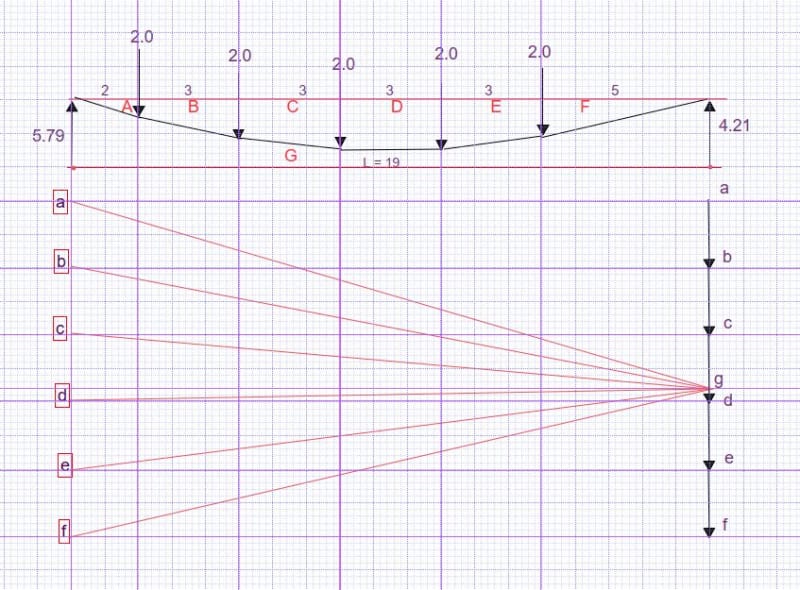
I made an attempt at drawing the funicular polygon...I followed the steps:
1. Draw the force vectors tip to tail (and to scale).
2. Define an arbitrary pole point
3. Connect the tip and tail of the force vectors to the pole to form the force diagram
4. Transfer parallel lines to the form diagram
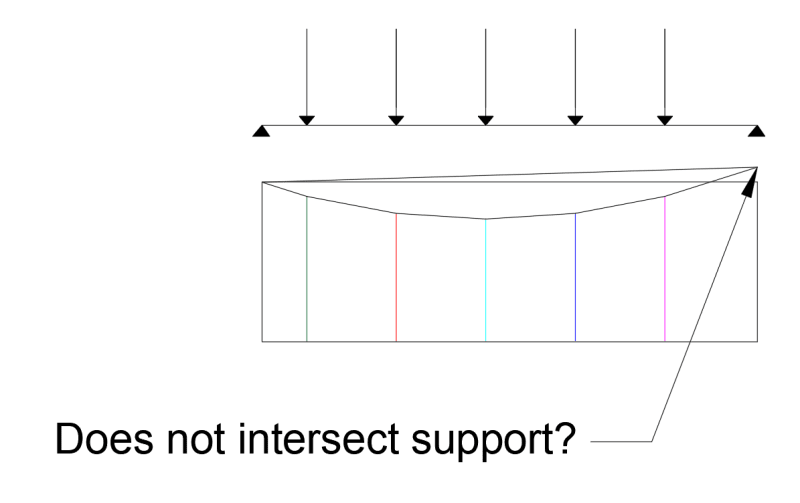
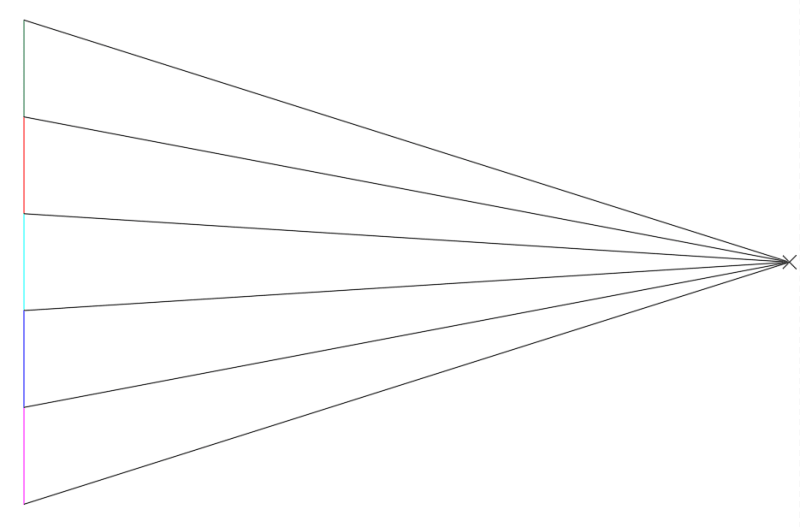
My question is, no matter where I draw the pole, I cannot get the funicular polygon to intersect both the left and right hand supports? Surely it must intersect these points as the funicular polygon represents the deformed geometry of a cable fixed to these supports?
Is there something obvious I am doing wrong in the formation of the funicular polygon?
Thanks in advance for any help!
I am new to the graphical static method used to draw funicular polygons but I see that it has tremendous value. I am trying to define the funicular shape of a beam under the action of five parallel point loads.
The point loads have equal magnitude but the spacing along the beam varies slightly. Supports at either end of the beam are pinned.

I made an attempt at drawing the funicular polygon...I followed the steps:
1. Draw the force vectors tip to tail (and to scale).
2. Define an arbitrary pole point
3. Connect the tip and tail of the force vectors to the pole to form the force diagram
4. Transfer parallel lines to the form diagram


My question is, no matter where I draw the pole, I cannot get the funicular polygon to intersect both the left and right hand supports? Surely it must intersect these points as the funicular polygon represents the deformed geometry of a cable fixed to these supports?
Is there something obvious I am doing wrong in the formation of the funicular polygon?
Thanks in advance for any help!