Radius1
Mechanical
- Jan 13, 2021
- 38
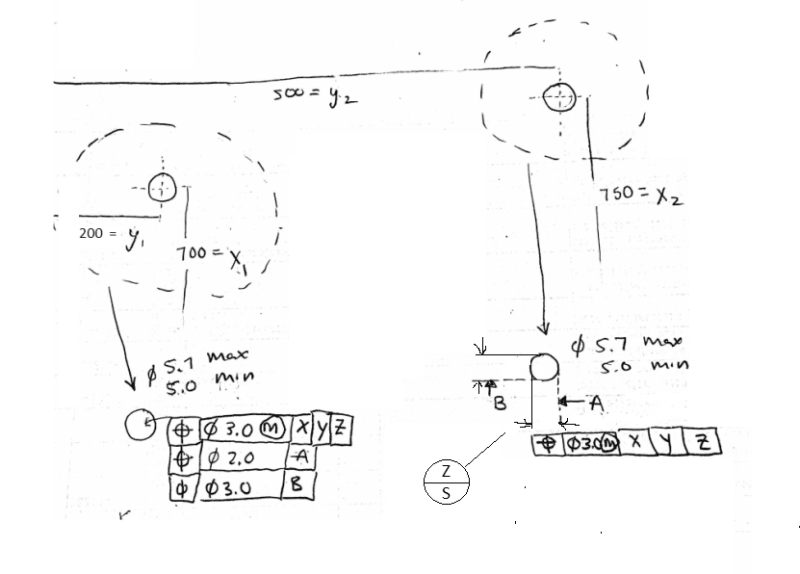
Two holes, diameter min = 5.0 , max = 5.7
Hole 1 coordinates 700 =x1 , 200 = y1
Hole 2 coordinates 750 =x2, 500=y2
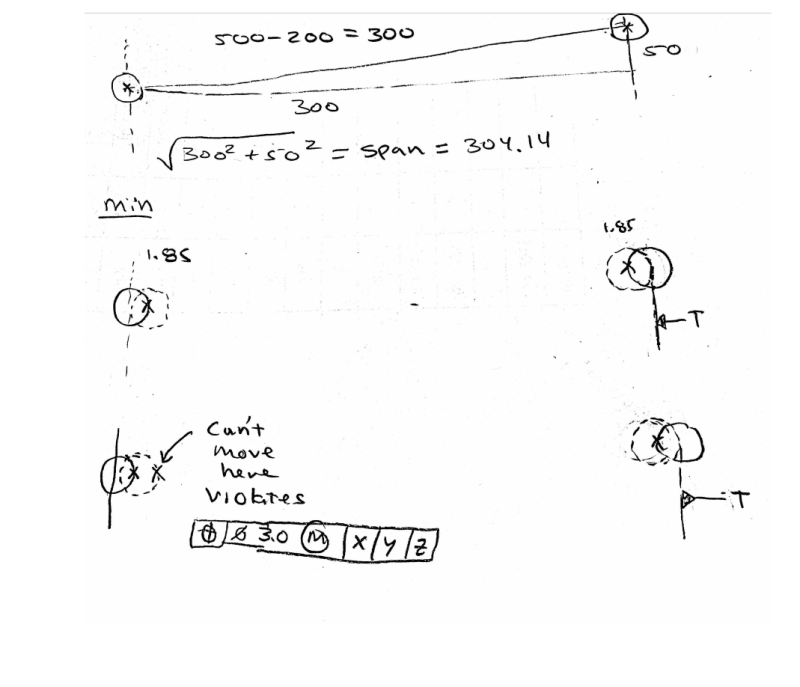
I am struggling how to find the min span of the holes with the given multiple segment position tolerance. The span will be the hypotenuse of the triangle formed by the holes. So the trig is easy, it's finding the min y, and x under the constraints of the positional tolerances that is challenging.
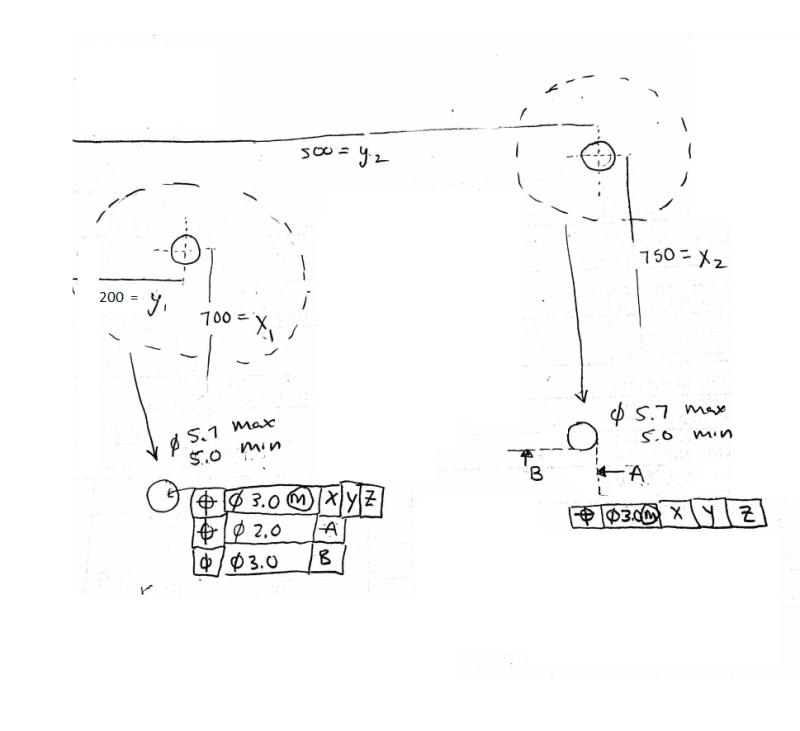
Hole 1 coordinates 700 =x1 , 200 = y1
Hole 2 coordinates 750 =x2, 500=y2
I am struggling how to find the min span of the holes with the given multiple segment position tolerance. The span will be the hypotenuse of the triangle formed by the holes. So the trig is easy, it's finding the min y, and x under the constraints of the positional tolerances that is challenging.


![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)