Hello, I'm a mechanical design engineer wanting to expand more into structural stress analysis and looking for some clarification on the determination and use of limit load, test loads, and margins.
My question is what actually is Limit Load and how are Margins calculated? See examples below.
The following information is taken from NASA-STD-5001 (Structural Design & Test Factors of Safety for Spaceflight Hardware):
[ul]
[li]Limit Load is "the maximum anticipated load, or combination of loads that a structure may experience during its design service life under all expected conditions of operation."[/li]
[li]"Design factors of safety and test factors shall be applied to the limit stress condition."[/li]
[li]Margin of Safety calculated by the following equation:
 [/li]
[/li]
[/ul]
I've also read the European equivalent standard which includes the same definition of limit load and a graphic illustrating factors application:
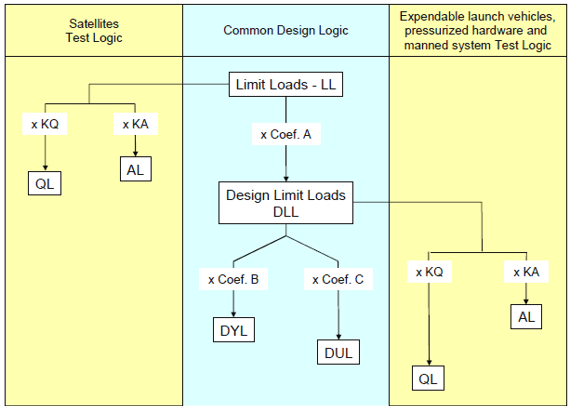
I have two example scenarios for which I'd like to understand what is what.
Example 1
A human-rated habitable pressure vessel is pressurized to a maximum 15 psi and proof pressure tested to 15 x 1.5 x 1.05 = 24 psi, where 1.5 = proof test factor from nasa-5001 and 1.05 = unknown environmental factor.
From the above documentation, qualification and acceptance test loads are the product of the limit load and test factors. In this example then, it would suggest the internal pressure of 15 psi is the limit load. This, however, in my mind is the "applied" load, and the resulting or calculated stress will be much higher than 15 psi and dependent on material, wall thickness, shape, etc. If I were to determine the margin in this example, it would seem the more appropriate equation would be:
MOS = (material strength / calculated stress * FS) - 1
So what is the limit load, MOS, and allowable here?
Example 2
Very similar to the first example, but more general.
Let's say a cantilevered beam is loaded at its free end by a load P. To test the beam strength given a FS of 1.5, you would load the beam to 1.5xP. Simple. Is "P" here the Limit Load since it's the maximum anticipated applied load and what is used to determine test factors? If so, it doesn't make sense to use this in the calculation of MOS. MOS equation has to include the resulting/calculated stress, otherwise would be independent of the actual structural design which of course doesn't make any sense.
What am I missing here?? Any feedback is much appreciated!
My question is what actually is Limit Load and how are Margins calculated? See examples below.
The following information is taken from NASA-STD-5001 (Structural Design & Test Factors of Safety for Spaceflight Hardware):
[ul]
[li]Limit Load is "the maximum anticipated load, or combination of loads that a structure may experience during its design service life under all expected conditions of operation."[/li]
[li]"Design factors of safety and test factors shall be applied to the limit stress condition."[/li]
[li]Margin of Safety calculated by the following equation:

[/ul]
I've also read the European equivalent standard which includes the same definition of limit load and a graphic illustrating factors application:

I have two example scenarios for which I'd like to understand what is what.
Example 1
A human-rated habitable pressure vessel is pressurized to a maximum 15 psi and proof pressure tested to 15 x 1.5 x 1.05 = 24 psi, where 1.5 = proof test factor from nasa-5001 and 1.05 = unknown environmental factor.
From the above documentation, qualification and acceptance test loads are the product of the limit load and test factors. In this example then, it would suggest the internal pressure of 15 psi is the limit load. This, however, in my mind is the "applied" load, and the resulting or calculated stress will be much higher than 15 psi and dependent on material, wall thickness, shape, etc. If I were to determine the margin in this example, it would seem the more appropriate equation would be:
MOS = (material strength / calculated stress * FS) - 1
So what is the limit load, MOS, and allowable here?
Example 2
Very similar to the first example, but more general.
Let's say a cantilevered beam is loaded at its free end by a load P. To test the beam strength given a FS of 1.5, you would load the beam to 1.5xP. Simple. Is "P" here the Limit Load since it's the maximum anticipated applied load and what is used to determine test factors? If so, it doesn't make sense to use this in the calculation of MOS. MOS equation has to include the resulting/calculated stress, otherwise would be independent of the actual structural design which of course doesn't make any sense.
What am I missing here?? Any feedback is much appreciated!
