Help with my non-standard gearing 2

[Lttlcheeze]

This may be simple to some, but this is my first experience with designing gears, so bear with me...

I'm trying to "cut" a spur gear to match the profile of the pinion gear I designed. This gear won't carry any load, it's basically for esthetics, but I want good contact between the two gears.

I have an 8 tooth pinion & 60 tooth spur gear.
Here is my pinion gear:

I am working with one tooth profile and trying to simulate it moving out of the mating gear. Seems simple enough...

This is the shape of one tooth, and the line/arc segments are something I drew that approximates what I should end up with (I used the assembly and adjusted the points until it was close).

I could just use those line segments, but I really want to figure this out mathematically.

This is what I figured should be right, but obliviously it's not...
-I drew a circle around the main gear with a radius of the distance between my gear shafts.
-Keeping the center of the pinion gear tooth coincident with that circle I rotated it 5 degrees (I plan on making this increment smaller once I get the calculation figured out).
-Then I rotated the tooth around the center of the spur gear at the increment that it would rotate if the pinion rotated that 5 degrees.
That was .6666666667 degrees. My math:
60 tooth spur - 8 tooth pinion
1 rotation = 7.5 rotations
360 degrees = (360 * 7.5) 2700 degrees
2700 / 5(sketch increment) = 540
360 / 540 = .666666667

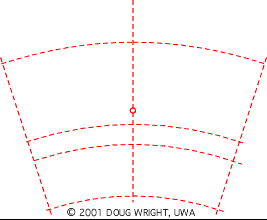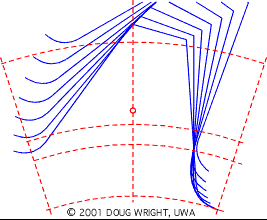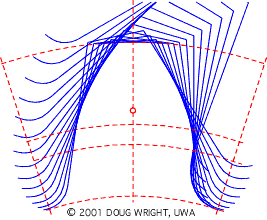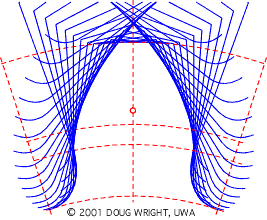
I'm sure I’m over simplifying this because here is my result:

The red line is the line/arc that represents where I should be.

I know it's really cluttered, but I figure once I get this figured out I can just use this file as a template.

So obliviously .66666667 is too much of an increment.

Just playing with the numbers I found .59 is really close to what I need. But I don't know how to get there mathematically.

Does anyone know if I'm just completely over simplifying this, or am I doing something wrong in the math????

Please help!!

Thanks,
Bill

Not sure if it will work but I also attached a .gif depicting what I'm trying to accomplish.

 

[gearcutter]

Google 'conjugate action of spur gears'.
There you'll learn the fundamental laws of gear-tooth action what you need to apply to spur gears for there to be constant velocity between mating profiles.
There are several profiles that can do this.
The involute family of curves are the easiest to calculate and manufacture as all involute profiles are derived from the same basic rack profiles (straight sides).
Unfortunately the profile you have come up with doesn't look anything like an involute; to me it looks more cycloidal. This will pose a manufacturing challenge.

Ron Volmershausen
Brunkerville Engineering
Newcastle Australia

http://www.aussieweb.com.au/email.aspx?id=1194181

 

[Occupant]

It depends on how you wany yo accomplish this. In Autocad it is relatively easy using script files based on the same principle that you showed. The picture that I downloaded are of two elliptical gears that have the added challenge that not only does the tooth form change with the radius of curvature, but also opposing flanks on the same tooth are different.

 

[gamjr]

As mentioned by gearcutter, a "matching" form can be found for your profile that will produce conjugate action (constant velocity ratio). The now standard involute tooth form has the added advantage of maintaining a constant pressure angle throughout the meshing action of any tooth pair. The result is, that for a constant transmitted torque, fatigue-inducing tangential and radial tooth load variations approach zero (for perfectly manufactured teeth). This is a biggie for modern high speed machinery.

 

[Lttlcheeze]

Well I've figured it out. So for anyone else trying to draw odd gears here it is. And it's rather simple...

The Movement of the Pinion Tooth Around the Main Gear is this:
360 / Nm = Tm (Nm=Number of Teeth on Main Gear, Tm=Angle Between Teeth on Main Gear)
Tm / X = M (X=Increment Factor, M=Increment Around Main Gear)

And for the Pinion:
360 / Np = Tp (Np=Number of Teeth on Pinion Gear, Tp=Angle Between Teeth on Pinion Gear)
Tp + Tm = Y
Y / X = P (X=Increment Factor, M=Increment Around Pinion Gear)

So from my original post:
Main Gear is 60t, Pinion is 8t
360 / 60 = 6 / 12 = .5 (I drew 20 teeth and linked them, and with the increment factor set at 12, the 20th tooth was just outside the main gear max OD, so I had plenty of steps inside to cut a good profile)
360 / 8 = 45 + 6 = 51 / 12 = 4.25

As I drew it, each tooth is rotated around the center of the main gear .5 deg.

Then the C/L of each tooth is rotated 4.25 deg. from the last.

That's it plain n simple. I've already made a few gears using this and it works every time.