Hello everyone,
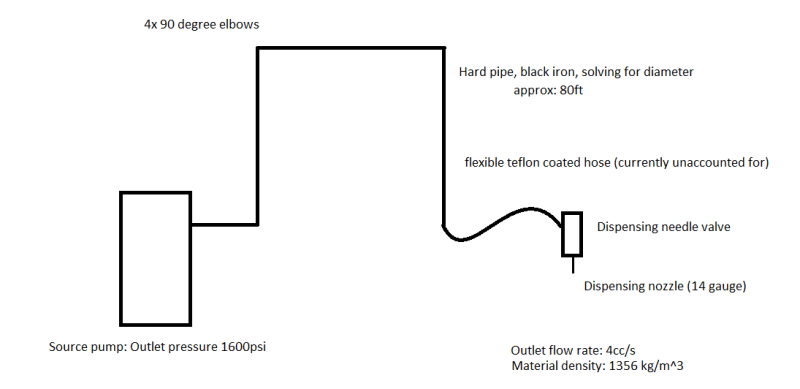
I'm working on a problem in which I am trying to recommend a hard pipe diameter to a customer for a (relatively) high viscosity non-newtonian fluid.
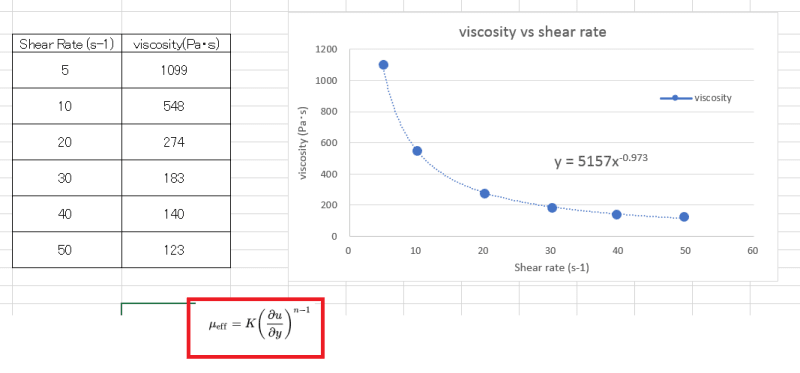
I am treating it as a power law fluid and have obtained constants K and n to describe the viscosity in relation to shear rate. I also have desired discharge flow rate, inlet pressure (outlet pressure is zero, right? It's being dispensed from a nozzle.), approximate pipe length, and nozzle size.
I've written some python code in order to help my calculations and here's where my issue is coming in. The Reynold's number I'm getting is on the order of 10^-6 which raised a red flag, and, my friction factor is about 9,000,000 so another major red flag. I am using 64/Re for the friction factor calculation. Using a different equation for friction factor like colebrook can give me a more reasonable friction factor, but doing so also yields a suggested pipe diameter that is far too small (based on practical experience).
Anyway, I'm not sure if I'm approaching this problem right at all, as I'm treating it as almost entirely a pipe flow problem. I think I probably don't have the right terms in my equations to account for the heavy neck down to the 14 gauge nozzle, but I can't seem to dig up any relevant information.
Here is my code:
Which results in:
all of which seems reasonable except for the friction factor and Reynold's number of course, but I'm looking at it from my undergrad fluids perspective where we never looked at fluids this viscous or flows this slow.
Any help or tips would be greatly appreciated!
Thank you.
I'm working on a problem in which I am trying to recommend a hard pipe diameter to a customer for a (relatively) high viscosity non-newtonian fluid.
I am treating it as a power law fluid and have obtained constants K and n to describe the viscosity in relation to shear rate. I also have desired discharge flow rate, inlet pressure (outlet pressure is zero, right? It's being dispensed from a nozzle.), approximate pipe length, and nozzle size.
I've written some python code in order to help my calculations and here's where my issue is coming in. The Reynold's number I'm getting is on the order of 10^-6 which raised a red flag, and, my friction factor is about 9,000,000 so another major red flag. I am using 64/Re for the friction factor calculation. Using a different equation for friction factor like colebrook can give me a more reasonable friction factor, but doing so also yields a suggested pipe diameter that is far too small (based on practical experience).
Anyway, I'm not sure if I'm approaching this problem right at all, as I'm treating it as almost entirely a pipe flow problem. I think I probably don't have the right terms in my equations to account for the heavy neck down to the 14 gauge nozzle, but I can't seem to dig up any relevant information.
Here is my code:
Python:
import sympy as sp
import numpy as np
delP = 1.1032 * (10**7) # Pascals
rho = 1355.92 # kg/m3
Q = 4 * (10**-6) # m3/sec
L = 24.38 # m
n = 0.027 # constant obtained from viscosity vs shear rate plot
K = 5157 # constant obtained from viscosity vs s hear rate plot
# D = sp.symbols('D') # diameter with inches to meter conversion factor
d = sp.Symbol('d') # inverse diameter (inverse because solver is having problems with D in denominator)
pi = np.pi
v = Q/((pi/4) * ((1/d)**2))
# average velocity expression from flow-rate and diameter
Re = ((((1/d)**n)*(v**(2-n))*rho)/(K*(((1+(3*n))/4*n)**n)*(8**n-1)))
# Reynolds number expression for power law fluids (darcy friction factor)
# f = 16/Re
f = 64/Re # Darcy friction factor
k11 = 798.9 # Friction loss factors
kinf1 = 0.3939
k12 = 300
kinf2 = 0.1
k13 = 1000
kinf3 = 0.25
kf1 = (k11/Re) + kinf1*(1+d)
kf2 = (k12/Re) + kinf2*(1+d)
kf3 = (k13/Re) + kinf3*(1+d)
inv_diameter = sp.nsolve((-delP/rho) + (2*f*(v**2)*L*d) + 4*(kf1*(v**2)/2) + (kf2*(v**2)/2) + (kf3*(v**2)/2), d, 1000)
# Solving for inverse diameter
d = inv_diameter
D = (1/inv_diameter)*39.37 # Diameter, in inches
v1 = Q/((pi/4) * ((1/inv_diameter)**2)) # velocity in mm/s
Re1 = ((((1/inv_diameter)**n)*(v1**(2-n))*rho)/(K*(((1+(3*n))/4*n)**n)*(8**n-1))) # Reynolds number
f1 = 64/Re1 # Darcy friction factor
print('Velocity in mm/s is ', v1*1000)
print('Reynolds number is ', Re1)
print('The friction factor is ', f1)
print('Pipe diameter in inches is', D)Which results in:
Python:
Velocity in mm/s is 1.06398183679041
Reynolds number is 6.58862657597730e-6
The friction factor is 9713708.80743941
Pipe diameter in inches is 2.72385109750467all of which seems reasonable except for the friction factor and Reynold's number of course, but I'm looking at it from my undergrad fluids perspective where we never looked at fluids this viscous or flows this slow.
Any help or tips would be greatly appreciated!
Thank you.