ship69
Mechanical
- Nov 23, 2015
- 22
Hello
I am new. I have simple a mechanical design problem:
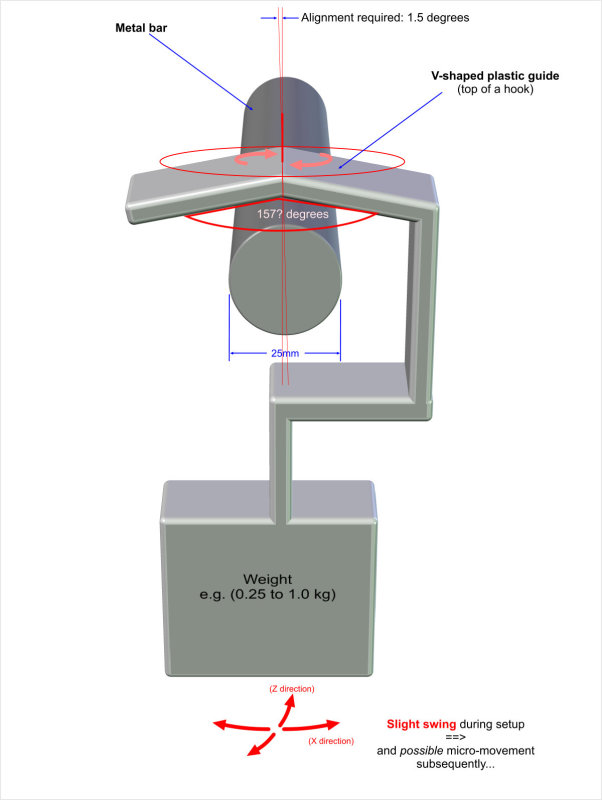
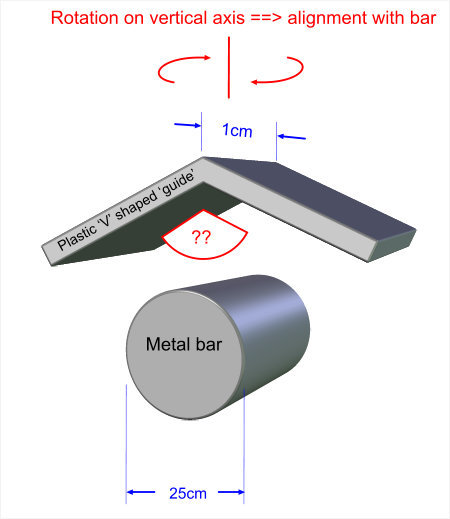
1. I have a cylinder - i.e. a round bar - that is 25mm in diameter and made of polished metal (chrome).
2. I have an inverted V shaped guide made from smooth plastic (probably polyethyline PE or similar. This inverted V will be fairly short - only 10mm (1cm) deep.
Now, the plastic inverted V shaped guide will be resting (unsupported) on top of the round bar, with a light force equivalent to say 200 grams, and it will be able to twist along a vertical axis.
My question is this:
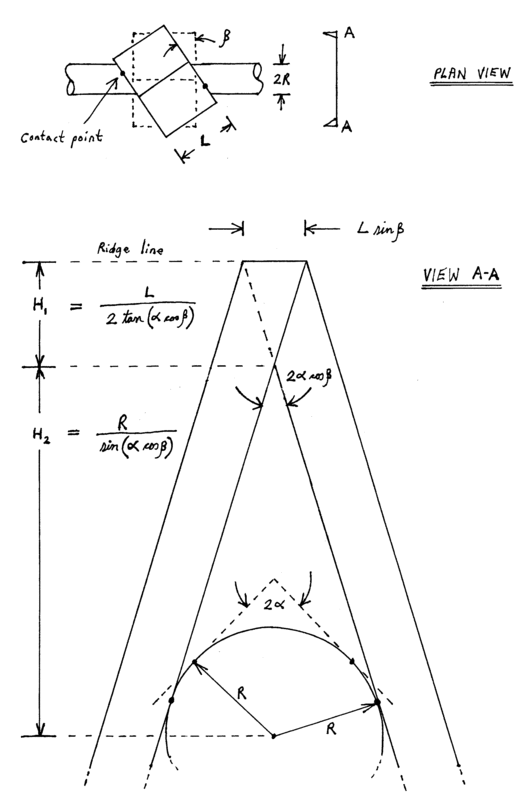
How shallow can I allow the angle of inverted 'V' to be and still expect the V to rotate so as to align with the direction of the metal bar? i.e. to point in the same direction. (The alignment of the two objects only needs to be within a few degrees)
To explain:
If the V is extremely steep say 45 degrees - or even 90 degrees - then it would be reasonable to expect the V to align EXACTLY with the bar. But if the V is very shallow and starts to approach 180 degrees, then one would not expect the V to rotate at all.
Are there any rules of thumb or guestimates that I could use?
J
P.S. Please excuse the very crude nature of the attached diagram, but I hope it brings the problem to life...
I am new. I have simple a mechanical design problem:
1. I have a cylinder - i.e. a round bar - that is 25mm in diameter and made of polished metal (chrome).
2. I have an inverted V shaped guide made from smooth plastic (probably polyethyline PE or similar. This inverted V will be fairly short - only 10mm (1cm) deep.
Now, the plastic inverted V shaped guide will be resting (unsupported) on top of the round bar, with a light force equivalent to say 200 grams, and it will be able to twist along a vertical axis.
My question is this:
How shallow can I allow the angle of inverted 'V' to be and still expect the V to rotate so as to align with the direction of the metal bar? i.e. to point in the same direction. (The alignment of the two objects only needs to be within a few degrees)
To explain:
If the V is extremely steep say 45 degrees - or even 90 degrees - then it would be reasonable to expect the V to align EXACTLY with the bar. But if the V is very shallow and starts to approach 180 degrees, then one would not expect the V to rotate at all.
Are there any rules of thumb or guestimates that I could use?
J
P.S. Please excuse the very crude nature of the attached diagram, but I hope it brings the problem to life...