Rohan K
Mechanical
- Oct 8, 2023
- 3
Hi members,
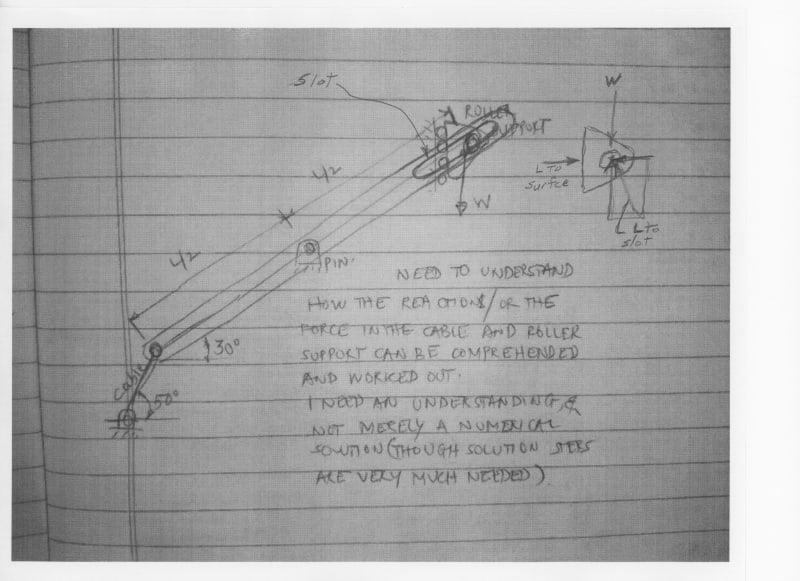
Rohan here and I am a Mechanical Engineer. Recently encountered a situation with a mechanism which could be compared conceptually to seemingly simple linkage where restoring forces for equilibrium need to be calculated.
But after trying to solve for the unknown forces I found that the no.of equations for equilibrium do not suffice to evaluate the no.of unknown forces/reactions keeping the link in static equilibrium.
I need to understand the concept behind the approach to the solution to such cases where unknown forces outnumber the available equations and seemingly make the problem statically indeterminate (correct me if I'm wrongly interpreting this after seeing the attached figure).
Kindly help me understanding the concept behind this (any explanation from anyone/reference book with such cases/book/etc.) is more than welcome and if someone can shed some light on the F.B.D. of the case and steps hinting to equations/solution is needed and highly regarded.
The figure indicating the case is attached for your reference.
Thanks and regards,
Rohan
Rohan here and I am a Mechanical Engineer. Recently encountered a situation with a mechanism which could be compared conceptually to seemingly simple linkage where restoring forces for equilibrium need to be calculated.
But after trying to solve for the unknown forces I found that the no.of equations for equilibrium do not suffice to evaluate the no.of unknown forces/reactions keeping the link in static equilibrium.
I need to understand the concept behind the approach to the solution to such cases where unknown forces outnumber the available equations and seemingly make the problem statically indeterminate (correct me if I'm wrongly interpreting this after seeing the attached figure).
Kindly help me understanding the concept behind this (any explanation from anyone/reference book with such cases/book/etc.) is more than welcome and if someone can shed some light on the F.B.D. of the case and steps hinting to equations/solution is needed and highly regarded.
The figure indicating the case is attached for your reference.
Thanks and regards,
Rohan