phoenixMetal
Mechanical
I am trying to determine how to calculate the force necessary to permanently deform a certain sheet metal item which has some bends.
Here is an image of the part:
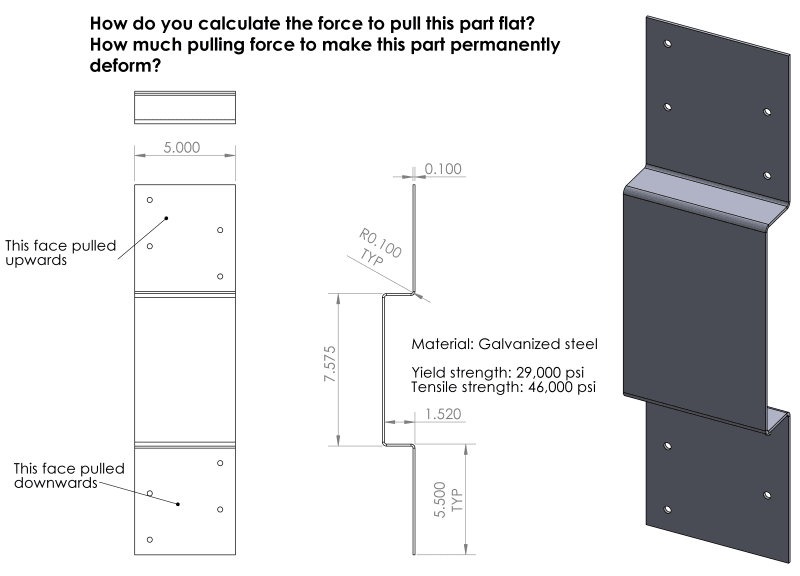
If there was a force that pulled the upper and lower halves apart (pulling in the direction that would flatten out the part if pulled hard enough), I'd like to know how to calculate that force.
I am not just looking to find out the numerical answer for this particular part. I am looking to learn the formula for how this sort of thing can be calculated for any similar part which may have more or less bends, different thickness, etc.
It is OK to assume that the flat areas of the part are perfectly rigid, so that we are talking about the deformation happening only in the bend regions. It is also OK to make any other reasonable shortcuts or simplifications to get a ballpark calculation.
The question could also be framed in any of the following ways - if you can more readily determine how to calculate for any of these scenarios:
1)How to calculate the force needed to permanently deform the part any amount?
2)How to calculate the force needed to deform (pull apart) the item by 0.1 inches (or any other arbitrary amount), with the deformation not necessarily being permanent.
3) How to calculate the force needed to pull the part substantially flat?
Part dimensions and mechanical properties for this example:
Material: Steel sheet
Yield strength: 29,000 psi
Ultimate tensile strength: 46,000 psi
Material thickness: 0.1"
Part width: 5"
Let me know if you have any questions and thank you for your help!
Here is an image of the part:

If there was a force that pulled the upper and lower halves apart (pulling in the direction that would flatten out the part if pulled hard enough), I'd like to know how to calculate that force.
I am not just looking to find out the numerical answer for this particular part. I am looking to learn the formula for how this sort of thing can be calculated for any similar part which may have more or less bends, different thickness, etc.
It is OK to assume that the flat areas of the part are perfectly rigid, so that we are talking about the deformation happening only in the bend regions. It is also OK to make any other reasonable shortcuts or simplifications to get a ballpark calculation.
The question could also be framed in any of the following ways - if you can more readily determine how to calculate for any of these scenarios:
1)How to calculate the force needed to permanently deform the part any amount?
2)How to calculate the force needed to deform (pull apart) the item by 0.1 inches (or any other arbitrary amount), with the deformation not necessarily being permanent.
3) How to calculate the force needed to pull the part substantially flat?
Part dimensions and mechanical properties for this example:
Material: Steel sheet
Yield strength: 29,000 psi
Ultimate tensile strength: 46,000 psi
Material thickness: 0.1"
Part width: 5"
Let me know if you have any questions and thank you for your help!
