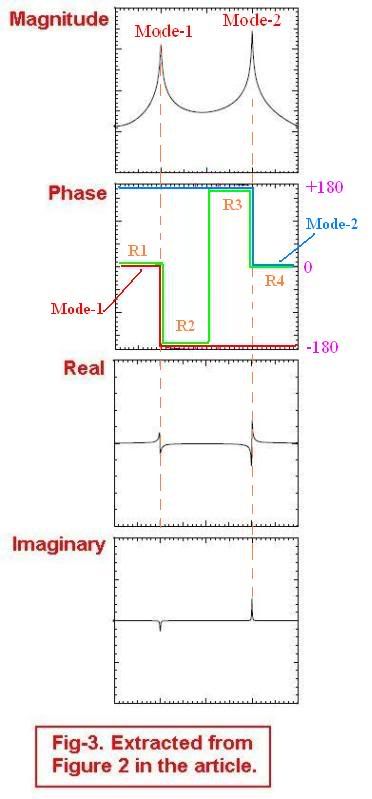
Let's say RED curve is the phase plot of Mode-1, BLUE curve is the phase plot of Mode-2, and GREEN is the effective phase plot. Please correct me if my plot is wrong. If my plot is correct, I'm wonder why at R1, when Mode-1 and Mode-2 are out of phase 180 degrees, why the effective phase follows the phase plot of Mode-1 instead of that of Mode-2. Ditto to that at R4 as well.
I have read the paper closer and I'm still pretty sure the 360 degree change is an artifact.
I think it convenient to imagine that each lightly damped peak has a "polarity". As Greg said, consider the polarity to be the sign of the transfer function of the mode immediately to the left of the peak.
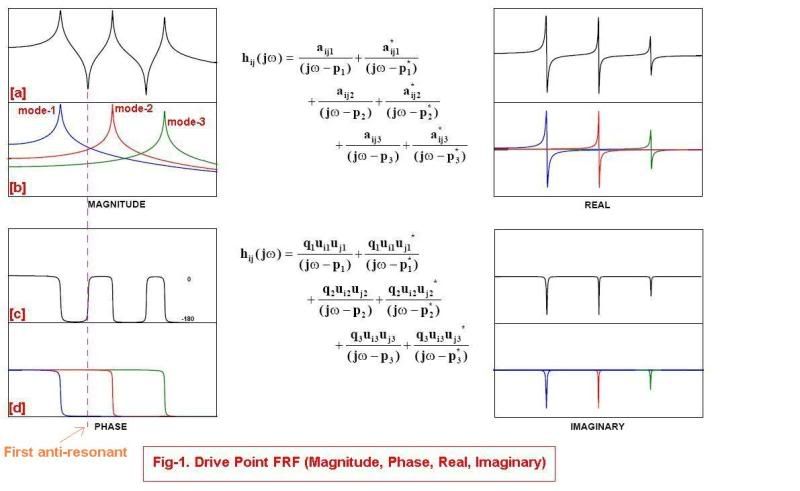
If it is a driving point impedance (point of measurement is same as point of force), then all peaks have the same "polarity". This can be inferred by recognizing that each peak in driving point impedance represents a simple SDOF lightly damped system. For a SDOF system, the displacement is in-phase below resonance and lags by 180 degrees above resonance. More generally and two sets of modes which have the same sign residue have the same polarity.
Let's assume the first resonance has simple positive (*) polarity and 2nd resonance also has simple positive polarity (*by positive polarity I mean just like SDOF, response is positive in-phase below resonance and negative out-of-phase below resonance). In the area just above first resonance, we know the response is dominated by the 1st resonance and so the FRF is negative. In the area just below the 2nd resonance, we know the response is dominated by the 2nd resonance and so the FRF is positive. So we know there has GOT to be a zero (antiresonance) between the 1st and 2nd resonance as the response turns from negative back to positive. And so it is for any two adjacent modes with same polarity we need a zero between. If two adjacent modes have opposite polarity, then no zero in between.
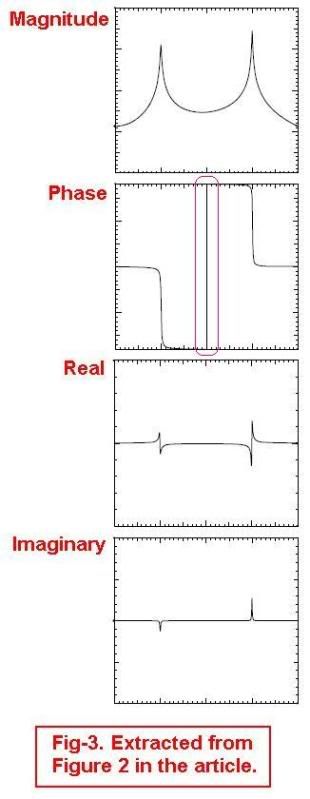
The total response is generally governed by only the two closest peaks. So for driving point impedance where each peak has the same polarity, we have zero's between all modes. This behavior can be seen on all the diagonal graphs of figure 2 which represent driving point impedances where you can see the "sharp" bottoms representing zero's (anti-resonances). In contrast the non-driving point (off-diagonal) graphs for this system have flat bottoms representing minima (saddle points) where adjacent peaks have opposite polarities and therefore no sign reversal is needed between peaks. I don't think it is always the case that off-diagnoal elements necessarily have saddle points as opposed to zero's (is it?).
Now let's look at the off-diagonal graphs of figure 2. They all have only 2 peaks. I believe it is a general property that by performing a cross-impedance measurement (excite and monitor at different points), we always reduce the degrees of freedom of the equivalent system as seen at the terminals where we measure / excite. (Maybe someone can comment further). At any rate it seems pretty obvious the two peaks have opposite polarity (you can see his imaginary portions have opposite sign). So there is no sign reversal required between peaks and we have a simple saddle point. The 360 degrees is a plotting artifact. If you didn't have it you would decrease below the bottom of the scale so they needed a 360 degree correction to keep it on the scale.
As far as your phase plots, let's label the scale: –180 at the bottom, 0 in the middle, 180 at the top. I think your mode 1 phase plot is correct. I think your mode phase 2 plot drawn in blue shuld be drawn starting at the bottom of the plot and then transitioning to 0 at the mode 2 resonance. Then the composite (total) phase is 0 below mode 1, -180 between modes 1 and 2 and 0 above mode 2.
My terminology + and – is a little simplistic since actually we are dealing with a complex quantity. However for lightly damped systems where modes do not overlap this is more than adequate and simplifies the discussion to make it easier to understand (for people like me). In the paper you linked, he uses the sign of the imaginary part to play the same role that I have used for + and -.
That's the way I see it but I may be wrong. If so hopefully someone will chime in.
An interesting note about who decides to response to what question. I think it is human nature you will respond to a question that is interesting or challenging. FRF plots are not something I totally understand and so it's interesting to me. I guess for these other guys it is old hat. Another aspect of human nature I observe on the forums, people are more likely to chime in to prove someone wrong than to help someone asking a question. That's fine also... I think I would do it myself if the question and incorrect response seemed trivial to me. If such is the case here I look forward to someone telling me if I'm wrong... maybe I'll learn something.
=====================================
Eng-tips forums: The best place on the web for engineering discussions.