Incorrect joule heat dissipation in transient thermal-electric analysis

[vepawz]

I'm trying to model a Resistance Spot Welding process using an implicit and transient thermal-electric problem on ABAQUS and came across this problem. Here's a simple test case in which i replicated the problem.

Consider the following axisymmetric analysis (no heat flows in or out of the system; any heat generated by the electric current stay within the system):

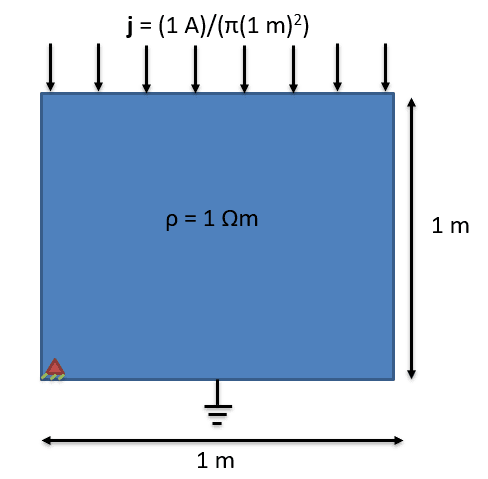
For a current of 1 A the current density is 0.318 A/m^2. For resistivity of 1 ohm-m, the resistance is 0.318 ohm. Consequently the voltage i get is also 0.318 V (IR = 1 A*0.318ohm).

The expected energy dissipated (let's call it 's') is (current_density)^2*resistivity*volume = 0.101*1*3.14 = 0.318 J

For a time-period of 1 s, I used the following fixed time increments to obtain the corresponding results:

Δt = 1 s : s = 0.105 J (one increment)
Δt = 0.5 s : s = 0.211 J (two increments)
Δt = 0.25 s : s = 0.264 J
Δt = 0.1 s : s = 0.296 J
Δt = 0.05 s : s = 0.307 J
Δt = 0.01 s : s = 0.316 J
Δt = 0.05 s - 1 s : s = 0.307 J (for automatic time control with initial time increment of 0.05 s)

Why does Δt = 1 s under predict the energy? Why is it that the first time increment always only output a third of total energy it should?

Any help is appreciated. Thanks.

 

[FEA way]

It may seem rather unusual since the documentation says that too small (not too large) time increments can cause problems and there's no upper limit. However I think that single increment in such transient coupled analysis is not enough to obtain valuable results. I came across somewhat similar issue in transient thermo-mechanical simulations of additive manufacturing processes. In case of these analyses small enough time increments are necessary to resolve temperature changes.

 

[vepawz]

@FEAway thanks for the reply. Ignoring the temperature change, the electrical energy dissipated (I explicitly set the Joule Heat Fraction to 1 just to be sure) which acts as the source of heat for temperature rise should not depend on the time step though. According to ABAQUS documentation, only the thermal part of the coupled thermal-electric analysis is time-dependent.

 

[FEA way]

This is really interesting. Can you share the input file of this analysis so that I could perform some test and try to figure out what causes these differences ? Is that some kind of benchmark or textbook problem for which you have the description ?

 

[vepawz]

@FEA way, I figured it out. It's to do with the way ABAQUS averages electrical power over a time increment in a transient analysis.

It computes power by integrating the electric field over the increment. In doing so, it uses the electric field at the end of the increment and the change in electric field over the increment. Consequently, it assumes zero initial voltage and thus Eⁿ⁺¹ and ΔE are equal.

dP = (Eⁿ⁺¹.σ^E.Eⁿ⁺¹ - Eⁿ⁺¹.σ^E.ΔE + (1/3)ΔE.σ^E.ΔE) dV
dP = (1/3)ΔE.σ^E.ΔE dV

 

[vepawz]

That was just a toy problem I created to understand the coupled thermal-electric analysis better.

 

[vepawz]

On that note, do you know how I can import voltages from result file?