Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Inner Boundary (IB) of an External Spherical Feature of Size 1
- Thread starter Tarator
- Start date
- Status
- Not open for further replies.
CH,
Perfect form is not technically required per rule #1, however a sphere is a special case due to the swept spheres definition of size. Neither a sphere of MMC size nor a sphere of LMC size may be violated. The secondary effect of this is that perfect form is technically required at both MMC and LMC for a sphere.
For a spherical feature, the limits of size dictate that the as-produced feature must exist in the volume between the two solids G(Sl,BrLMC) and G(Sm,BrMMC) where Sl and Sm are 0 dimensional spines (points). The effect is that which I described above. Neither a sphere of size MMC or size LMC may be violated.

Perfect form is not technically required per rule #1, however a sphere is a special case due to the swept spheres definition of size. Neither a sphere of MMC size nor a sphere of LMC size may be violated. The secondary effect of this is that perfect form is technically required at both MMC and LMC for a sphere.
By definition, perfect form at LMC is not required, so there is no "LMC sphere" it's enough to have "LMC measurements" which are all 8mm.
For a spherical feature, the limits of size dictate that the as-produced feature must exist in the volume between the two solids G(Sl,BrLMC) and G(Sm,BrMMC) where Sl and Sm are 0 dimensional spines (points). The effect is that which I described above. Neither a sphere of size MMC or size LMC may be violated.

CheckerHater
Mechanical
chez311,
You have to read same standard but little further, actually next paragraph.

No LMC sphere still.
"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future
You have to read same standard but little further, actually next paragraph.

No LMC sphere still.
"For every expert there is an equal and opposite expert"
Arthur C. Clarke Profiles of the future
Burunduk
Mechanical
- May 2, 2019
- 2,580
CH said:Burunduk,
You described it twice, but would you be so kind to draw it?
How exactly "dent" and "bump" look like?
Here is how a dent and a bump look like:

And That's how a dent on a spherical thing looks like. Imagine there is an equal bump on the opposite side.
Apparently, if the nicely-formed portion of the sphere of the OP example is of a uniform 8mm diameter then as chez311 suggests the sphere I described fails the size requirement per Y14.5.1. It still conforms to the Y14.5 Actual local size definition though - so it is up to the manufacturer or QA department - depends if they bother beyond 2 point measurements of size.
CH,
That statement is an extrapolation of the fact that for a feature controlled at MMC, Sl is not required to be of perfect form. For a cylindrical and width shaped features having 1 and 2 dimensional spines respectively means that Sl is not required to be a line or plane. There is still an LMC sphere swept in both cases, even though perfect form is not required. No allowances for a different interpretation for spheres is provided even though the term imperfect form does not make sense for a 0 dimensional spine ie: point as there is no possible form variation of a point, so we must sweep an LMC sphere along a 0 dimensional spine (point) which results in a single sphere of LMC size.
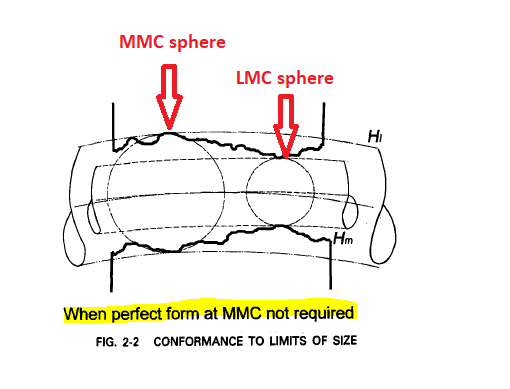
That statement is an extrapolation of the fact that for a feature controlled at MMC, Sl is not required to be of perfect form. For a cylindrical and width shaped features having 1 and 2 dimensional spines respectively means that Sl is not required to be a line or plane. There is still an LMC sphere swept in both cases, even though perfect form is not required. No allowances for a different interpretation for spheres is provided even though the term imperfect form does not make sense for a 0 dimensional spine ie: point as there is no possible form variation of a point, so we must sweep an LMC sphere along a 0 dimensional spine (point) which results in a single sphere of LMC size.

- Thread starter
- #25
I made this table to show the options:
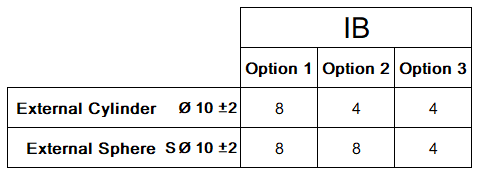
In my opinion, it is Option 2.
- For an external cylinder: The LMC would be a cylinder, where each cross-section would be a perfect circle of dia 8. According to Rule #1, this cylinder is allowed to deform (bend, twist) within a cylinder of dia 12 (MMC cylinder). If that happens, the IB will be 4.
- For an external sphere: The LMC would be a perfect sphere of dia 8. Based on Rule #1, this sphere must reside in a sphere of dia 12 (MMC sphere). However, you cannot possibly deform a sphere and yet maintain the minimum material (keeping the actual local size 8). Any type of deformation would add material, hence the sphere would not be at its LMC. In other words, a sphere at its LMC will always be a perfect sphere. So the IB will be 8.

In my opinion, it is Option 2.
- For an external cylinder: The LMC would be a cylinder, where each cross-section would be a perfect circle of dia 8. According to Rule #1, this cylinder is allowed to deform (bend, twist) within a cylinder of dia 12 (MMC cylinder). If that happens, the IB will be 4.
- For an external sphere: The LMC would be a perfect sphere of dia 8. Based on Rule #1, this sphere must reside in a sphere of dia 12 (MMC sphere). However, you cannot possibly deform a sphere and yet maintain the minimum material (keeping the actual local size 8). Any type of deformation would add material, hence the sphere would not be at its LMC. In other words, a sphere at its LMC will always be a perfect sphere. So the IB will be 8.
Burunduk
Mechanical
- May 2, 2019
- 2,580
Tarator,
I agree, except for the bolded portion which you wrote in brackets:
I agree, except for the bolded portion which you wrote in brackets:
It would not fail the actual local size, it would fail the size limits per the swept spheres requirement. The actual local size measured between opposed points can still be not less than 8 everywhere and in spec. So it eventually depends on what part of the industry those involved belong to - do they evaluate size by two-point measurements or do they sweep spheres.Tarator said:However, you cannot possibly deform a sphere and yet maintain the minimum material (keeping the actual local size 8).
- For an external cylinder: The LMC would be a cylinder, where each cross-section would be a perfect circle of dia 8. According to Rule #1, this cylinder is allowed to deform (bend, twist) within a cylinder of dia 12 (MMC cylinder). If that happens, the IB will be 4.
The Y14.5.1 description of this imperfect cylinder per the swept spheres interpretation is a perfect sphere of LMC size swept along an imperfect spine(curve). This swept solid must exist entirely within the material of the feature. I agree the worst case boundary (cylinder of perfect form which is not violated by this imperfect swept solid) is 4 no matter how we define IB in context of a feature lacking applied geometric controls.
In other words, a sphere at its LMC will always be a perfect sphere. So the IB will be 8.
Refer to my (6 Aug 20 13:25) post. It depends on how we define IB in the context of a feature lacking applied geometric controls. Per Y14.5-2009, if we assume IB is even applicable, I can see an argument saying its still 4. Per 2018 I think its pretty clear it would be 8.
- Thread starter
- #28
Burunduk
Mechanical
- May 2, 2019
- 2,580
Tarator,
A sphere produced with all its actual local sizes at the LMC limit and imperfect form can have the same amount of material as a sphere produced at the LMC diameter and perfect form.
As I've been explaining, it's a matter of having a protruding "compensation" across every cavity.
A sphere produced with all its actual local sizes at the LMC limit and imperfect form can have the same amount of material as a sphere produced at the LMC diameter and perfect form.
As I've been explaining, it's a matter of having a protruding "compensation" across every cavity.
- Thread starter
- #30
Burunduk,
A sphere made at its LMC must be perfect. If it has any "bumps", that would add material, so you can't say the sphere is at its LMC. If it has "dents", that would remove material and force at least one actual local size to be less than 8.
The same would also apply to a circular feature of size. Can you please show me a circle made at its LMC (dia 8) and that is imperfect?
A sphere made at its LMC must be perfect. If it has any "bumps", that would add material, so you can't say the sphere is at its LMC. If it has "dents", that would remove material and force at least one actual local size to be less than 8.
The same would also apply to a circular feature of size. Can you please show me a circle made at its LMC (dia 8) and that is imperfect?
-
1
- #31
Burunduk
Mechanical
- May 2, 2019
- 2,580
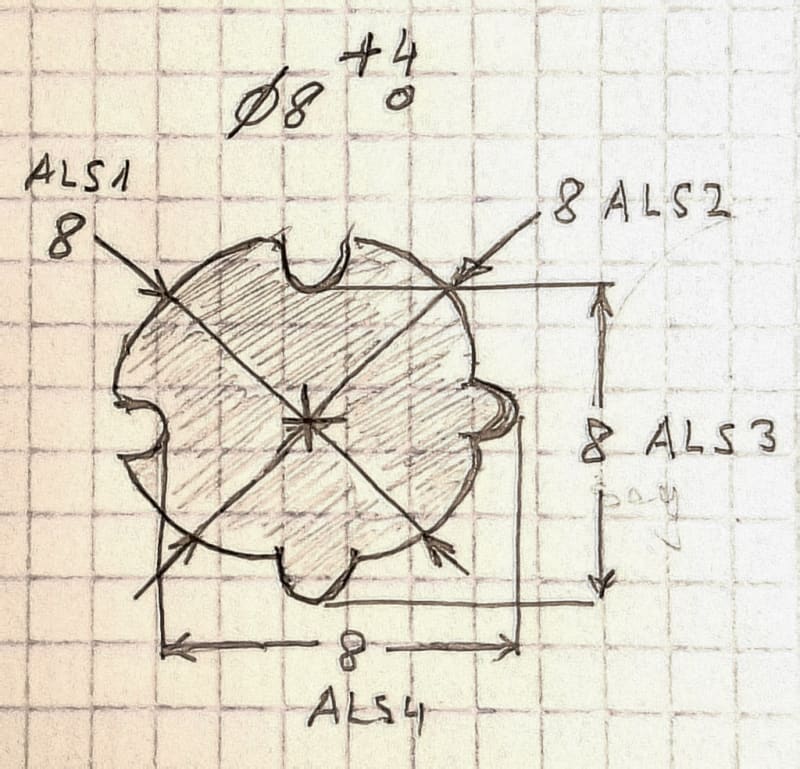
Tarator, see the graphic above. It illustrated an as-produced feature designed nominally circular.
Every actual local size on the circular element (could be a cross-section through the center of a sphere) is exactly 8mm and not less. Purely per the Y14.5 meaning of limits of size (Actual Local Size) the feature is within spec. It is measured as distances between opposed points. This is also how the majority of the industry works.
Some will point again towards Y14.5.1 and say that the swept spheres concept is the final word. But the discrepancies between the standards are the problems of the committee, not the user's fault. It is also not that important that the definition of actual local size is somewhat incomplete - two point measurements are a well-established concept in the industry.
- Thread starter
- #32
Burunduk
Mechanical
- May 2, 2019
- 2,580
Tarator, no problem. Glad to provide any useful insight. 4 as the IB is also my suggestion but it is still somewhat controversial from the reasons mentioned in the different posts in this thread; namely the absence of the implied rule #1 form error allowance from the Inner Boundary definition that in the 09' version only mentions "stated" geometrical tolerances as factors added to the size tolerance to generate the boundary, and the other thing is the swept spheres concept.
- Thread starter
- #34
Burunduk,
I see the definition of IB can cause hesitation. Let's call it the Smallest Worst-Case Boundary... My intention is to be able to use it in a tolerance stack-up analysis for a min. wall thickness problem for example. What the name is would not matter much.
- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 6
- Views
- 10K
- Replies
- 25
- Views
- 3K
- Locked
- Question
- Replies
- 16
- Views
- 5K
- Locked
- Question
- Replies
- 20
- Views
- 9K
- Locked
- Question
- Replies
- 9
- Views
- 5K

![[thumbsup2] [thumbsup2] [thumbsup2]](/data/assets/smilies/thumbsup2.gif)