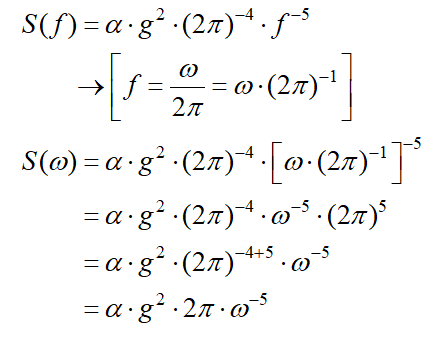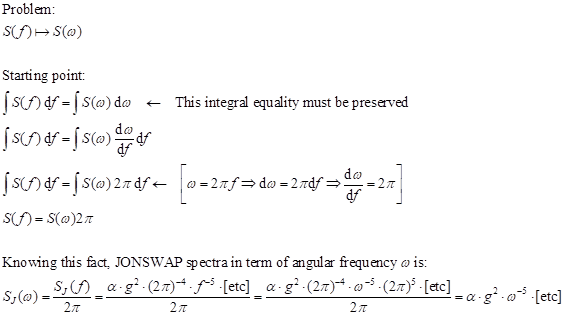JONSWAP spectum S(w)

[Giu.seppe]

Hello to all. Sorry for my english, I'm an italian civil engineering student.
I have a question about the JONSWAP spectrum. We know that the JONSWAP spectrum, in terms of frequency, is:

S(f) = α g² (2π)^-4 f^-5 exp {-1.25 (f_m/f)⁴} γ^{exp {-(f-f_m)2/(2σ2f_m2)}}

Now I would like to write S in term of ω: f= ω/(2π). The first piece of S (f) becomes:

S(ω) = α g² (2π)^-4 f^-5 [etc.]

= α g² (2π)^-4 [ω/(2π)]^-5 [etc.]

= α g² (2π)^-4 ω^-5 (2π)⁵ [etc.]

= α g² (2π) ω^-5 [etc.]

The problem is that in all the books (and also on Wikipedia) it is written:

S (ω) = α g² ω^-5 [etc.]

without the remaining 2π in my passages. What am I missing?

Thanks for your help!

 

[IRstuff]

So, where did you get your version? Since you're the anomaly... would you argue with MIT?

http://web.mit.edu/13.42/

http://www/handouts/wave_spectra_slides2.pdf

Nevertheless, since it's in frequency space, it's likely that the putative Fourier transform's form is different, and the pesky 2π is often floating around as a square root term in symmetrical FT's or only in one direction. The only thing you can be certain about with FT is FT^-1[FT(f] = f, i.e., the 2π term resolves itself when taking the inverse FT of an FT'd function



TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Giu.seppe]

Thanks for your answer.

So, where did you get your version?

First of all in original Hasselmann paper (pag. 32). Other references:

[ul]
[li]BENASSAI, Introduction to coastal dynamics and shoreline protection, par. 2.2.3 (pag. 100)[/li]
[li]OCHI, Ocean waves, par. 2.3.5 (page 45)[/li]
[li]SORENSEN, Basic wave mechanics for coastal and ocean engineers, par. 6.3.3 (pag. 138)[/li]
[li]USACE, Shore protection manual, vol. 1 (pag. 3-43)[/li]
[/ul]

 

[IRstuff]

One check would be to integrate the total energy, the time integral and the frequency-space integrals per Parseval's theorem

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[chicopee]

It seems that there is a mistake in the third line. The second line shows f^5 whereas the third line shows the substitution f=w/2n as(w/2n)^-5. the -5 exponent should be a positive exponent unless further substitution in the original equation shows that you are correct.

 

[IRstuff]

OP's first and second limes are incorrect; it should have f^-5 as shown in the cited reference

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[IRstuff]

Note that Pierson-Moskowitz's original paper doesn't have a 2*pi term at all.

The bottom line is that if you can match the graphs, then you're done, regardless of the 2*pi

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Giu.seppe]

It seems that there is a mistake in the third line. The second line shows f^5 whereas the third line shows the substitution f=w/2n as(w/2n)^-5. the -5 exponent should be a positive exponent unless further substitution in the original equation shows that you are correct.

Sorry, I didn't understand. For more clarity, I write my passages

OP's first and second limes are incorrect; it should have f-5 as shown in the cited reference

Sorry, but (again) I didn't find the error you said...

 

[IRstuff]

Oh, OK, your minus signs in the exponents were obscured by the upper arms of the f's.

read

https://wikiwaves.org/Ocean-Wave_Spectra

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Giu.seppe]

Thanyk you so much!!! Question solved.
_____________________________________

References

[1] Ocean-Wave Spectra (on Wikipedia), url:

https://wikiwaves.org/Ocean-Wave_Spectra

[2] Fréchot, J. (2006). Realistic simulation of ocean surface using wave spectra, url:

https://hal.archives-ouvertes.fr/fi...ation_of_ocean_surface_using_wave_spectra.pdf