TooStressed
Mechanical
- Jan 28, 2022
- 7
Hello,
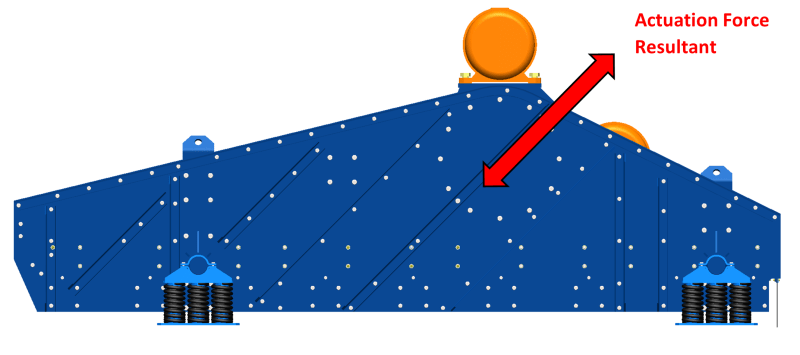
I am analyzing a material screening machine. It consists of a structure that is supported by springs. The assembly includes two motors with unbalanced masses that produce an excitation force which causes the structure to vibrate.
The motors operate at 1200 RPM (20 Hz).
As the structure is supported by springs, rigid body modes are present in the modal analysis and in reality. As expected, the effective mass fraction for each of the rigid body modes is near 1.0, with the rest of the modes having an extremely low effective mass fraction.
The modal analysis indicates modes at (or near) 40 Hz, 60 Hz, 80 Hz, 100 Hz. As these are multiples of the operating frequency, I am concerned. I'm sure that if I extract more modes I'll find many more multiples of the operating frequency. But how many modes are significant when the effective mass is dominated by the rigid body modes?
Should I artificially constrain the model? That will change the natural frequencies. How do I deal with that?
I am also concerned that while only a very small fraction of the total mass participates in a particular mode, it may be due to small component vibrating violently and increasing the stresses in the welds that attach it to the structure assembly.
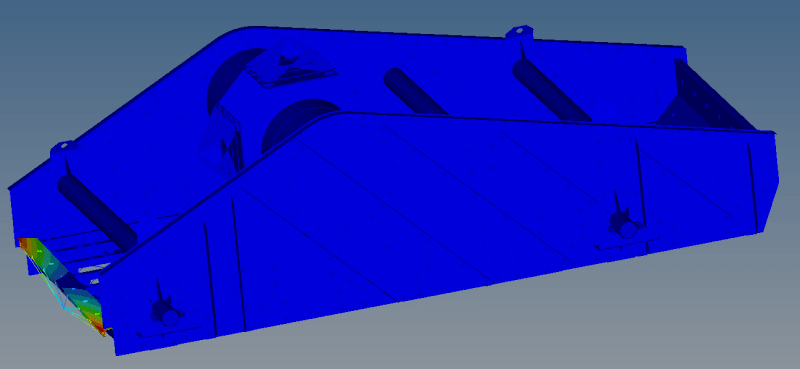
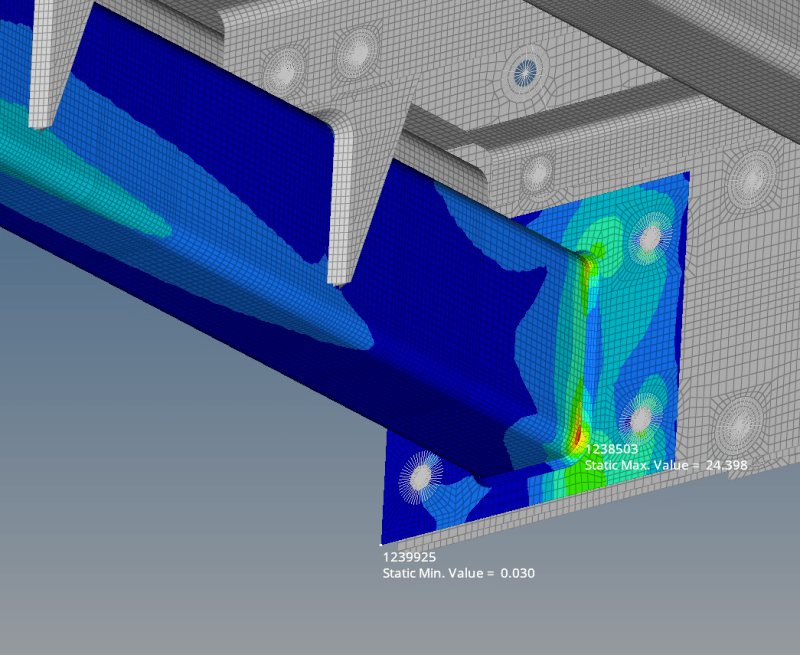
I also ran a quasi-static simulation with inertia relief and identified the regions of high stress.
How can I determine if the operating frequency will result in an intolerable increase in stress values?
Thank you.
I am analyzing a material screening machine. It consists of a structure that is supported by springs. The assembly includes two motors with unbalanced masses that produce an excitation force which causes the structure to vibrate.
The motors operate at 1200 RPM (20 Hz).
As the structure is supported by springs, rigid body modes are present in the modal analysis and in reality. As expected, the effective mass fraction for each of the rigid body modes is near 1.0, with the rest of the modes having an extremely low effective mass fraction.
The modal analysis indicates modes at (or near) 40 Hz, 60 Hz, 80 Hz, 100 Hz. As these are multiples of the operating frequency, I am concerned. I'm sure that if I extract more modes I'll find many more multiples of the operating frequency. But how many modes are significant when the effective mass is dominated by the rigid body modes?
Should I artificially constrain the model? That will change the natural frequencies. How do I deal with that?
I am also concerned that while only a very small fraction of the total mass participates in a particular mode, it may be due to small component vibrating violently and increasing the stresses in the welds that attach it to the structure assembly.
I also ran a quasi-static simulation with inertia relief and identified the regions of high stress.
How can I determine if the operating frequency will result in an intolerable increase in stress values?
Thank you.