7788_011
Structural
- Feb 7, 2022
- 24
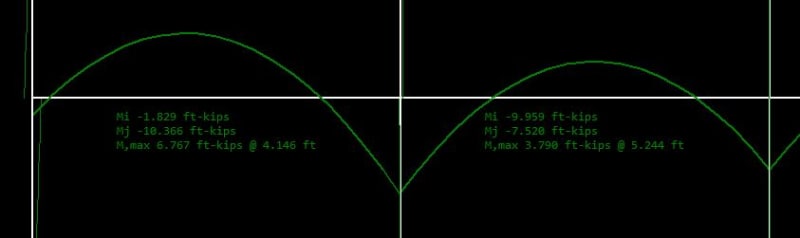
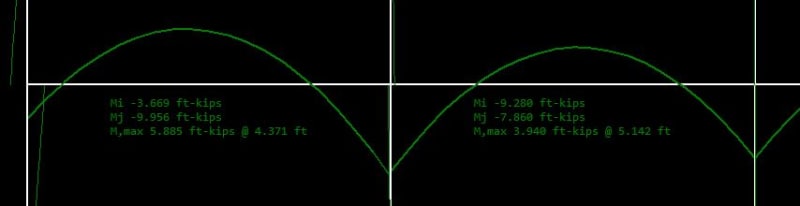
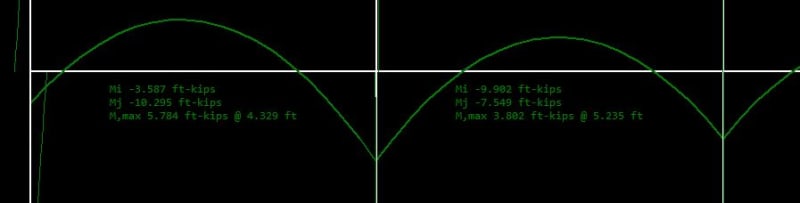
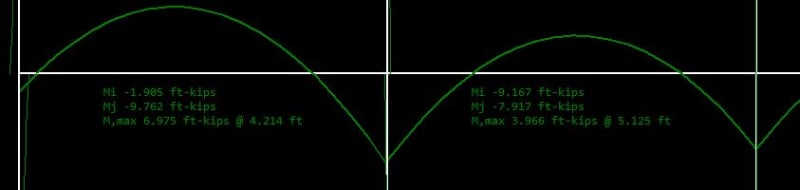
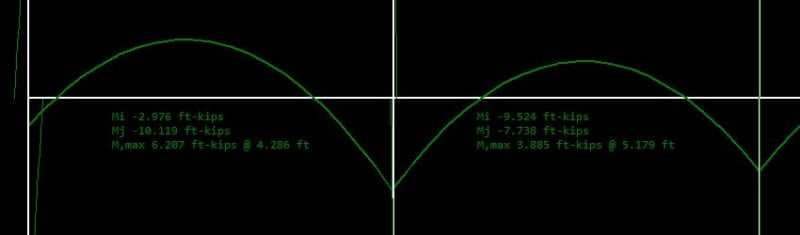
Given that for continuous concrete beams the moment generated at the supports will normally exceed the cracking moment Mcr of the beam, isn't it a must to increase the design bending moment & corresponding reinforcement at mid spans generated from a elastic frame analysis?
Can anyone please tell me how you consider this in you design? Do you compare the negative moment with Mcr and simply apply the positive moment at mid spans by a amplification factor (what factor is adequate if so?) or do you manually reduce the stiffness of the beam segement at supports in your analysis?
Can anyone please tell me how you consider this in you design? Do you compare the negative moment with Mcr and simply apply the positive moment at mid spans by a amplification factor (what factor is adequate if so?) or do you manually reduce the stiffness of the beam segement at supports in your analysis?