Hello,
I am new to the forums so I hope I am posting this in the correct forum.
I will try to explain the problem below:
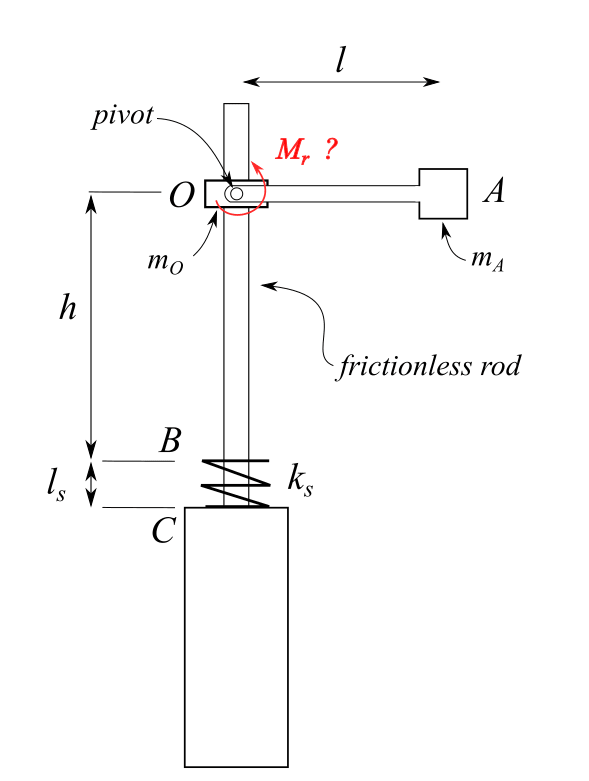
Link OA can pivot around O without friction.
Mass mO is left to free fall for height h guided by the frictionless rod until it hits spring ks.
Spring ks then deforms and any downward motion stops when it deforms completely (ls).
What would be the required moment Mr to prevent link OA from rotating when the motion stops?
What would be the best srategy to solve this problem?
Thank you!
I am new to the forums so I hope I am posting this in the correct forum.
I will try to explain the problem below:
Link OA can pivot around O without friction.
Mass mO is left to free fall for height h guided by the frictionless rod until it hits spring ks.
Spring ks then deforms and any downward motion stops when it deforms completely (ls).
What would be the required moment Mr to prevent link OA from rotating when the motion stops?
What would be the best srategy to solve this problem?
Thank you!


![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)
