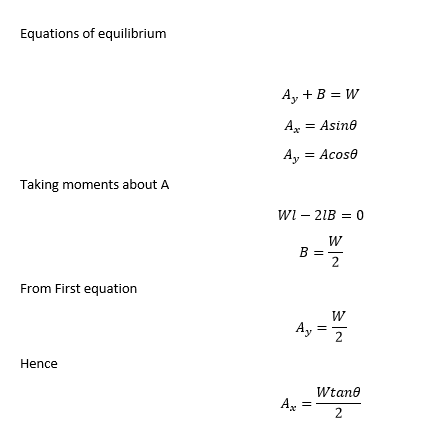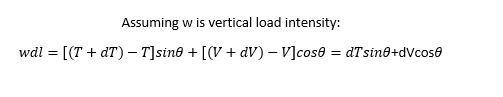Very detailed answer from JoshPlumSE. Here is my take:
[ul]
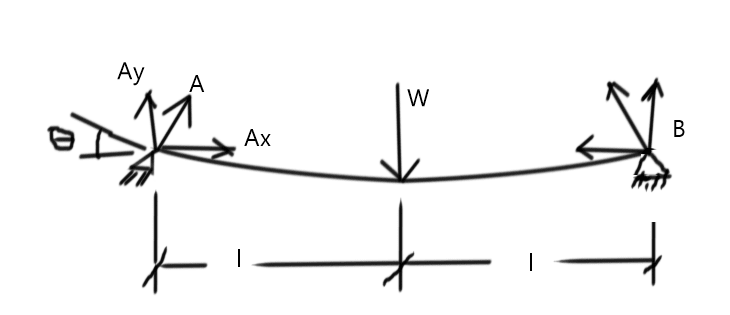
[li]The horizontal reaction exists, but is negligible for small deflections which is about 99% of the structures we deal with. Furthermore, simply-supported beam usually refer to pin-roller supports. It's hard to actually fully "clamp" a beam such that the ends do not translate at all[/li]
[li]For large-deflection problems like tensile structures, these horizontal reactions are what keeps the structure up. A tiny wire has negligible moment of inertia, yet it can resist a lot of load (e.g. horizontal lifelines) because it can deflect and form an axial load path. [/li]
[li]Most software do not pick up the horizontal component. Large-deflection analyses are difficult to do because you have to adjust the load increment dynamically to "form-find" the shape. Stiffness only starts to increase when the axial load path can start form (think about a sagging cable being deflected, the stiffness is almost zero initially which is tough for most programs to handle)[/li]
[/ul]
[ul]
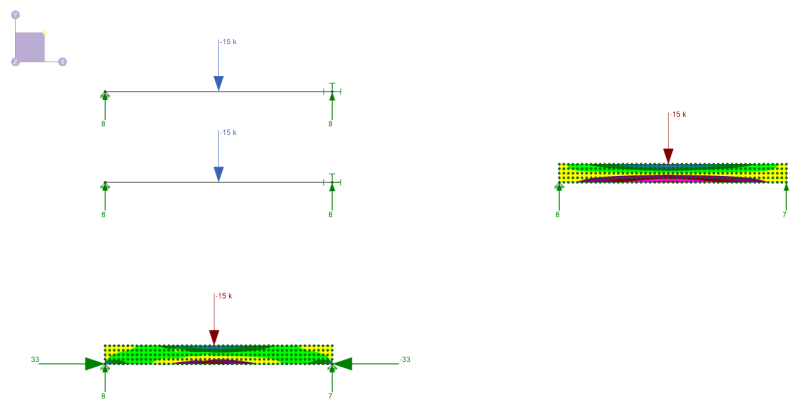
[li]Here is a screenshot of a test model in RISA. The top left beam is pin-pin, the beam below that is pin-roller. Both does not have a horizontal reaction because of small deflection assumption[/li]
[li]On the right, you can see a 2-D plate model with the same load and cross-section and pin-roller support. No horizontal reaction[/li]
[li]On the bottom is a 2-D plate model with pin-pin support. Look at the stress contour, notice how some arching action formed because of pin-pin rather than the conventional flexure theory. But realize that a pin-support assumes infinite rigidity to prevent horizontal translation, this is often not the case[/li]
[li]I didn't model it here, but you can also move the pin support to the neutral axis of the plates, in which case no horizontal reactions will form either[/li]
[/ul]