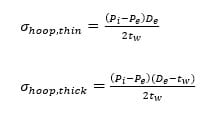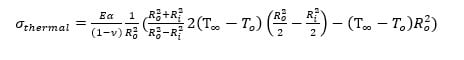mtz_engr
Aerospace
- Jan 6, 2022
- 19
Hoping to find someone that knows a bit more than I do on this matter.
I currently have a cylindrical geometry modeled and meshed with 2D Quad elements. This has been assigned Titanium material properties and a specified thickness. I have several load cases of combinations of internal pressure values (100 to 6900 psi) applied to the internal faces of the elements and temperatures values (-400 to 1000 deg F) applied to the nodes of the mesh. Both ends are fixed in translation and rotation. (intial temperature set as 70 deg F)
I started by performing a Linear Static solution to see what kind of results I got. I am interested in the tangential stress around the cylinder, because this is the principal stress and what should be the highest for this geometry. Interestingly enough, towards either end of the pipe, the stress values are highly negative (I am talking 100,000+ ... Saw -430,000 psi on one case) and the largest value seen towards the center is around 35,000 psi for the extreme case of pressure and temperature.
Doing hand calculations of the tangential stress causes by pressure and temperature, I arrive at around 93,000 psi for the combination of the hoop stress and thermal stress. I designed the geometry in the model to be able to handle this with a modest factor of safety.
Can anyone give me any indication of why the values I am getting in FEA are so strange? (Nonsensically negative towards the ends and positive but low towards the center)
Thanks in advance.
Using Patran/Nastran 2020
I currently have a cylindrical geometry modeled and meshed with 2D Quad elements. This has been assigned Titanium material properties and a specified thickness. I have several load cases of combinations of internal pressure values (100 to 6900 psi) applied to the internal faces of the elements and temperatures values (-400 to 1000 deg F) applied to the nodes of the mesh. Both ends are fixed in translation and rotation. (intial temperature set as 70 deg F)
I started by performing a Linear Static solution to see what kind of results I got. I am interested in the tangential stress around the cylinder, because this is the principal stress and what should be the highest for this geometry. Interestingly enough, towards either end of the pipe, the stress values are highly negative (I am talking 100,000+ ... Saw -430,000 psi on one case) and the largest value seen towards the center is around 35,000 psi for the extreme case of pressure and temperature.
Doing hand calculations of the tangential stress causes by pressure and temperature, I arrive at around 93,000 psi for the combination of the hoop stress and thermal stress. I designed the geometry in the model to be able to handle this with a modest factor of safety.
Can anyone give me any indication of why the values I am getting in FEA are so strange? (Nonsensically negative towards the ends and positive but low towards the center)
Thanks in advance.
Using Patran/Nastran 2020