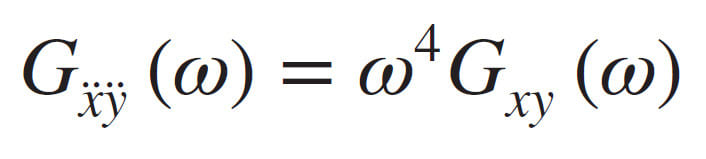Operational Modal Analysis: mode shape estimation from different type of measurement data 1

[harprah]

Hi everyone.

Operational Modal Analysis allows to estimate modal properties (natural frequencies, mode shapes, etc.) of a structure from ambient vibration tests. Several methods are developed to this aim: FDD, EFDD, SSI, etc. All methods require the measurement of the dynamic response of the structure. In general, it can be measured by means of different type of sensors, in terms of different kinematic quantities: acceleration, velocity, displacement or, even, strain.

My question concerns the estimation of mode shapes. I would like to know if the type of kinematic measured quantity affects the estimation of mode shapes. Specifically, I would like to know if mode shape estimated from acceleration measurement are the same of those estimated from displacement measurement.

Thank you!

 

[electricpete]

In an ideal linear world there is no difference. Mode shape by definition describes motion at a single sinusoidal frequency. The difference between displacement and acceleration characterizations of that single-frequency sinusoidal motion amounts to a constant scaling factor across all spatial points .... which does not affect the shape.

Practical differences may arise if you are using a sensor in a range that it becomes non-linear or unreliable.

=====================================
(2B)+(2B)' ?

 

[harprah]

Thank you very much! Your explanation is very clear.

In order to get a formal demonstration, do you think that it could be argued what follows?
Since power spectral density matrix of acceleration signals is for each frequency proportional to the power spectral density matrix of displacement signals (see attachment) and since "mode shape by definition exists only at a single frequency", the two mode shapes differ only for a constant scaling, which in OMA is unknown and therefore irrelevant.

 

[GregLocock]

Yup, that's the key. Each response would be scaled by the same conversion factor when moving between domains.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[GregLocock]

Incidentally we call them operating deflection shapes, ODS, not OMA, as they don't necessarily have the proper characteristics of a proper modal, such as being able to add them together at non resonant frequencies. The exception is if you strongly correlated inputs, but that leads to other problems. Anyway, fantastically useful technique when combined with hammer tests, and a great way of creating puzzles for the FEA boys.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[harprah]

Thank you GregLocock, very useful!!!

I knew that the basic peak picking method in frequency domain allows to estimate ODS; anyway, if I don't wrong, there are some OMA methods, like EFDD or SSI, that allow to estimate proper mode shapes. Isn't it?

 

[GregLocock]

So far as I know peak picking is the only sensible method. There probably are better ways, I'm tempted to say something based on complete ensemble empirical modal decomposition, but that's on the to do list! I don't actually do modals any more, I'm certainly not up to speed with what might be possible. I'm thinking of some sort of cross correlation between all the channels.

https://iopscience.iop.org/article/... and,treatment method for sequence interface.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[harprah]

ok GregLocock, your replies are very useful... thank you!!!

 

[GregLocock]

Or partial coherence?

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[harprah]

I suggest you to take a look to the following methods: Frequency Domain Decomposition (FDD); Enhanced Frequency Domain Decomposition (EFDD); and Stochastic Subspace Identification (SSI). These methods are very reliable and allow to estimate proper mode shapes. In particular, the basic idea of FDD is very simple and its implementation is straightforward!

 

[electricpete]

but that's on the to do list!

I thought you were retired. Or did I remember that wrong?

=====================================
(2B)+(2B)' ?

 

[GregLocock]

No, retiring at some point. I'm on 2.5 days a week.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[hacksaw]

Retiring, maybe, but still solving problems. Keep it up!