Rstructural
Structural
Hi All,
A question about the calculations for bursting reinforcement in AS3600/AS5100 (I'll refer to AS3600 as the clause is the same).
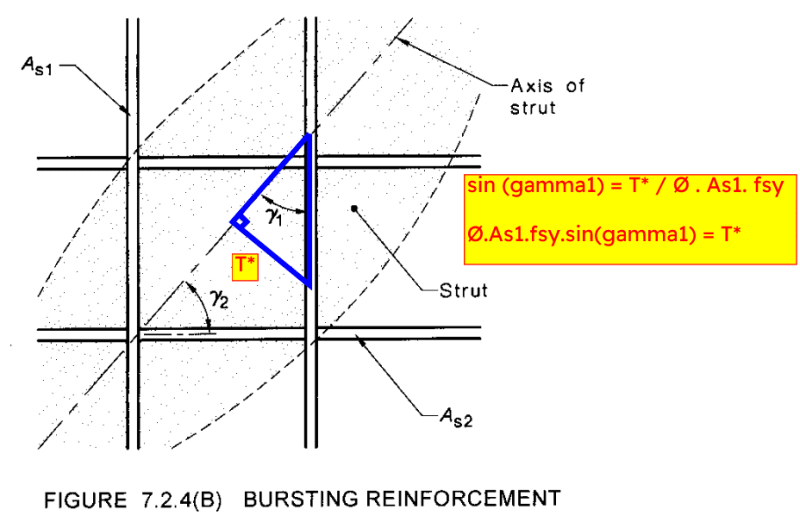
My understanding of the intent of Equation 7.2.4(3) is that there is a bursting force acting at some inclined angle, and in the case of providing orthogonal reinforcement, we are to provide vertical reinforcement to resist the vertical component of the bursting force and similar for the horizontal component.
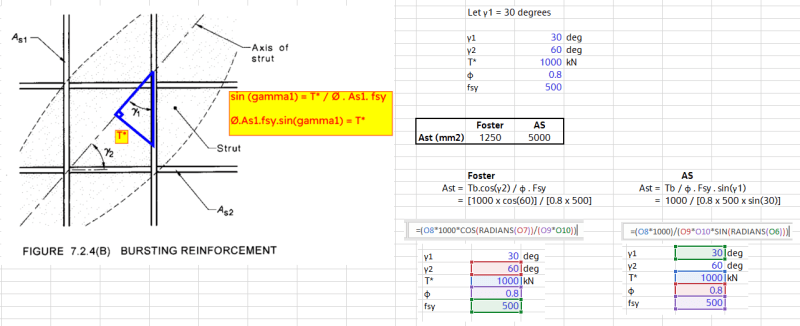
I've attached some notes which may be easier to read than equations in text form below.
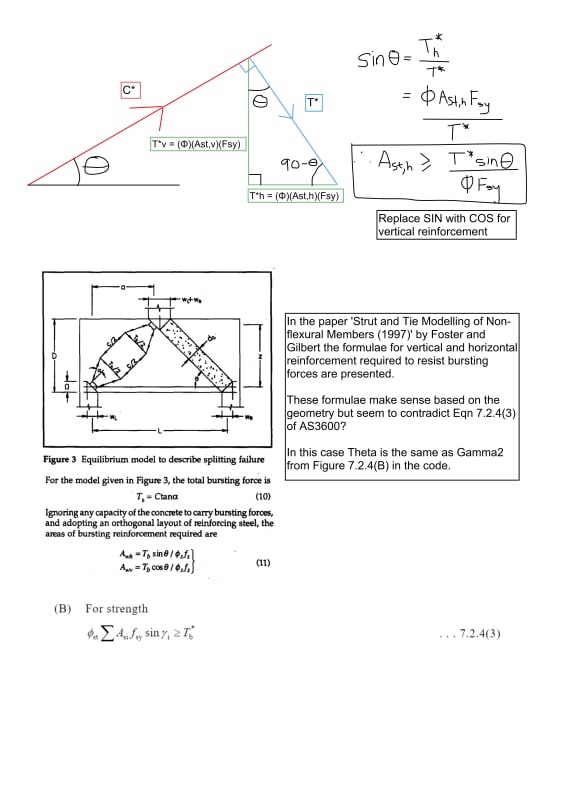
The bursting force acts perpendicular to the axis of the strut. Using the horizontal reinforcement case as an example, if the strut axis relative to the horiztonal plane is at some angle Theta then Sin(Theta) = [(Φ)(Ast,h)(Fsy)] / T* where (Φ)(Ast,h)(Fsy) is the force in the reinforcement to match the horizontal component of the bursting force.
Re-arranging the equation to find Ast gives Ast = [T* x Sin(Theta)]/[ΦFsy].
This is in agreement with Foster and Gilberts paper 'Strut and Tie Modelling of Non-flexural Members (1997)' as well as the Reinforced Concrete Basics textbook by Foster and co.
However, if you were to re-arrange the code Equation 7.2.4(3) you get Ast = T* / [(Φ)(Ast,h)(Fsy)(sin(Theta))] whereby sin(Theta) ends up on the denominator of the equation and based on Figure 7.2.4(B) the same angles are being used i.e Theta in this case is Gamma2 from the figure to correspond to As2, the horizontal reinforcement.
I feel I may be missing something obvious, but the equations from the Foster/Gilbert paper make sense to me and it would seem the left hand side of the code Equation should be divided by sin(Gamma) rather than multiplied? Would greatly appreciate if anyone could point out where I've gone astray.
Cheers.
A question about the calculations for bursting reinforcement in AS3600/AS5100 (I'll refer to AS3600 as the clause is the same).
My understanding of the intent of Equation 7.2.4(3) is that there is a bursting force acting at some inclined angle, and in the case of providing orthogonal reinforcement, we are to provide vertical reinforcement to resist the vertical component of the bursting force and similar for the horizontal component.
I've attached some notes which may be easier to read than equations in text form below.
The bursting force acts perpendicular to the axis of the strut. Using the horizontal reinforcement case as an example, if the strut axis relative to the horiztonal plane is at some angle Theta then Sin(Theta) = [(Φ)(Ast,h)(Fsy)] / T* where (Φ)(Ast,h)(Fsy) is the force in the reinforcement to match the horizontal component of the bursting force.
Re-arranging the equation to find Ast gives Ast = [T* x Sin(Theta)]/[ΦFsy].
This is in agreement with Foster and Gilberts paper 'Strut and Tie Modelling of Non-flexural Members (1997)' as well as the Reinforced Concrete Basics textbook by Foster and co.
However, if you were to re-arrange the code Equation 7.2.4(3) you get Ast = T* / [(Φ)(Ast,h)(Fsy)(sin(Theta))] whereby sin(Theta) ends up on the denominator of the equation and based on Figure 7.2.4(B) the same angles are being used i.e Theta in this case is Gamma2 from the figure to correspond to As2, the horizontal reinforcement.
I feel I may be missing something obvious, but the equations from the Foster/Gilbert paper make sense to me and it would seem the left hand side of the code Equation should be divided by sin(Gamma) rather than multiplied? Would greatly appreciate if anyone could point out where I've gone astray.

Cheers.