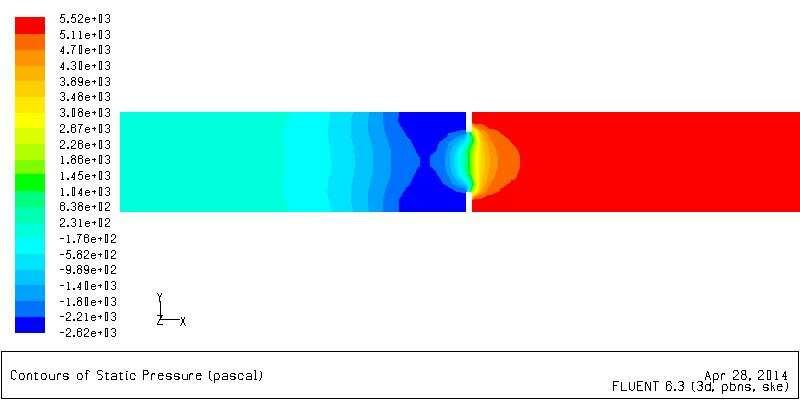
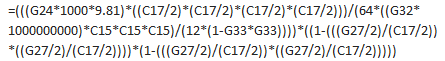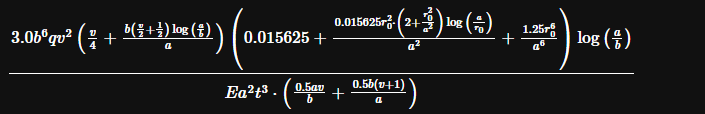Having joined a new company, I've been tasked to "standardise" a batch of old spreadsheets that are frequently reused. Absolutely nothing give references for the calculations embedded and I'm working to change that. I've managed to track down most of them, but have run into a wall relating to deflection of an orifice plate with a horrendous bit of excel that simplifies to this:
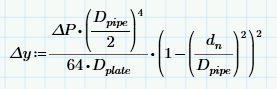
[delta]y = Axial deflection of plate inner edge
[delta]P = Differential pressure
Dpipe = Pipe ID, used as the fixed edge of the plate
Dplate = Plate constant/flexural rigidity
dn = Orifice ID
The values for this are essentially the same as using Roark's 7th Ed Table 11.2 Case 2e (for the range where it's practical to real-world circumstances), but I can't find where this much more compact equation comes from - any pointers?
Edit: Define [delta]y
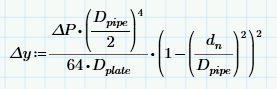
[delta]y = Axial deflection of plate inner edge
[delta]P = Differential pressure
Dpipe = Pipe ID, used as the fixed edge of the plate
Dplate = Plate constant/flexural rigidity
dn = Orifice ID
The values for this are essentially the same as using Roark's 7th Ed Table 11.2 Case 2e (for the range where it's practical to real-world circumstances), but I can't find where this much more compact equation comes from - any pointers?
Edit: Define [delta]y