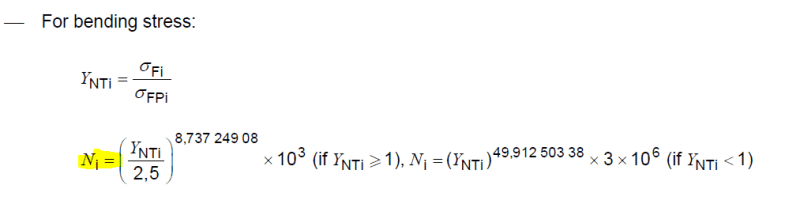Palgmer - Miner equation derivation 5

[namelessudhay]

Palgmer-Miner equation is used in ISO standard ISO 6336-6. I want to understand how it is derived. It helps to consolidate damage caused by multiple torque, cycle bins. A bin means a torque applied for a given number of cycle. As an outcome of the equation, a single equivalent torque that produces the total damage caused by multiple bins for the total number of cycles as original bins.

The equation is:

Pl. note that coordinates n1,T1; n2,T2 and n3,T3 do not need to be on the same line.

My objective is to derive the above equation. While I attempted to do that, I could progress to this level:

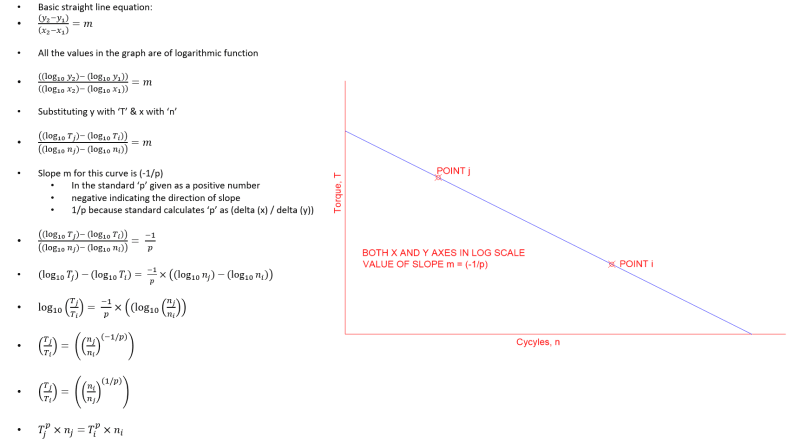
Can someone help to proceed further to reach until the equivalent torque formula given in the ISO standard? Many thanks in advance!

 

[rb1957]

have you tried "google" ? a search for "miner's rule fatigue analysis" produced many hits that looked relevant.


another day in paradise, or is paradise one day closer ?

 

[JStephen]

From what you have posted, it's not immediately obvious that it could be derived.
The last equation you have is of similar form with the summation sign.
It looks to me like somebody said "But what if we have different torques at different durations? Let's just prorate them this way."

 

[rb1957]

I too suspect that it is "experimentally" derived.

another day in paradise, or is paradise one day closer ?

 

[chicopee]

Is this equation applied to a single shaft; if not explain to us how is the shafting system assembled

 

[chicopee]

I am kicking myself for not recognizing the equation presented in the ISO standard. It is a weighted equation and you'll see weighted equations in calculus, contaminant concentration evaluation, industrial noise studies and in statistics.

 

[namelessudhay]

Dear all,

I am really sorry for not responding to your replies. Unfortunately, I didn't receive any email notifications and hence I assumed nobody replied to my question.

@Chicopee - This equation is applicable to any component that undergoes a fatigue load cycle a single gear, a shaft or a flange for example. Hence it is not relevant how the assembly is or is it a single or multi shafts

@rb1957 & @JStephen - May be true that it is experimentally derived. However such equations generally come with some constant value in the equation do not come so organized... I put a screenshot of an experimentally derived equation from the same standard for example:

So I still suspect this to be a derived equation.

@rb1957 - Of course I did a google search. I couldn't find anything useful to my question

 

[hydtools]

The equation for a straight line is y = mx + b where b is the y intercept at x = 0 and m is the slope. The OP equation is for calculating slope m.

Is the final derivation just equating the area under the curve to Teq*sum(n1+n2+..nn) ?

Ted

 

[namelessudhay]

Hi Hytools...
You are right, I should have named it "equation to find slope of a line"

And does sum of n*T^p give the area under the curve? (I am bad at maths... May be this answer will turn to be important)

 

[rb1957]

I'm confused. what's being asked ?

The title asks for a derivation of Miner's rule. I'm surprised that the simple google search yielded nothing … here are a couple of my responses …
1) Miner’s Rule and Cumulative Damage Models

https://www.weibull.com/hotwire/issue116/hottopics116.htm

Miner’s rule is one of the most widely used cumulative damage models for failures caused by fatigue. It is called 'Miner’s rule' because it was popularized by M. A. Miner in 1945. In this article, we will explain what it is and how it is related to other more advanced cumulative damage models in ALTA.

2) Miner's Rule | Aerospace Engineering

http://www.aerospacengineering.net/miners-rule

2013-07-23 · Miner’s rule is probably the simplest cumulative damage model. It states that if there are k different stress levels (with linear damage hypothesis) and the average number of cycles to failure at the ith stress, S i, is N i, then the damage fraction, C, is:. where: – n i is the number of cycles accumulated at stress S i. – C is the fraction of life consumed by exposure to the cycles at ...

3) Palmgren-Miner Rule - an overview | ScienceDirect Topics

https://www.sciencedirect.com/topics/engineering/palmgren-miner-rule

The Palmgren-Miner rule is a valuable tool in fatigue design, but it also has a few weak points that can limit its application if a high precision is required in the analysis. The most important disadvantage is that this approach does not account for the sequence in which the constant amplitude stresses occur. This sequence may not matter if the hydraulic gate is subjected to fatigue load ...

now I haven't looked at these, but they sound relevant ?

or is about that specific equation ?
I'd rearrange as Teq^p*sum(ni) = sum(Ti^p*ni) … so that Teq is the effective Torque(?) applied for the total number of cycles that is equivalent to a range of Torques, each applied for a number of cycles.


another day in paradise, or is paradise one day closer ?

 

[hydtools]

After individual cycles have been identified and the concept of fatigue damage is defined, a further simplification that is often performed is to present the load spectrum as a single ‘equivalent’ value (Dover, 1979). The concept is that the information from a stress histogram can be simplified into a single constant amplitude equivalent stress range value given by:

8.4
where

Ntot is the total number of cycles in a load history,

q is the total number of stress classes in the histogram,

∆σi is the stress range for stress class i,

ni is the number of cycles of size ∆σi and

m1is the slope of the S–N line used to assess fatigue life.

The equivalent stress range, ∆σeq, therefore represents a constant amplitude stress range that would give the same number of cycles to failure as the complex load history. As with the simple Palmgren–Miner rule, ∆σeq does not consider the complex interaction between cycles with different amplitudes and mean stresses. However, ∆σeq can be used as a method for reducing a complex stress history into a single number that is easily compared. For example, Samuelsson (1988) developed the twin concepts duty, which is a function of service life and ∆σeq, and capacity which depends on the global and local geometry of the weld. These are random variables that can be used to assess failure probabilities for complex welded structures.

The equivalent stress range concept in Eq. 8.4 is easily derived assuming a constant S–N slope and D = 1. Niemi (1997) has presented a modified form of Eq. 8.3 which allows the equivalent stress range to be computed for bi-linear S-N lines and for various values of D:

8.5
where

∆σk is the stress range associated with the knee observed during constant amplitude loading,

ni is the number of cycles of stress ∆σi where ∆σi > ∆σk,

nj is the number of cycles of stress ∆σj where ∆σj < ∆σk,

m1 is the slope of S–N line above the knee point,

m2 = m1 –1 is the slope of S–N line below the knee point and

D is the damage sum, e.g. D = 0.5.

The value ∆σeq computed from either Eqs. 8.4 and 8.5 can be used to compute life directly from an S–N line with constant slope m2 = m1 = 3.

The equivalent stress concept is the final simplification step for a variable amplitude time history. In each step some information is lost at the expense of convenience. Table 8.1 summarises the simplifying assumptions and the information lost. The first level of simplification, i.e. rainflow cycle counting, is nearly always performed. However, even this common step loses information on load frequency content which may be significant for corrosion fatigue studies or structures with potential vibration problems. Cycle sequence information is also lost, which may be important if mean stress changes occur at regular intervals or if cycle ranges vary according to a regular pattern. The loss of mean stress data associated with the second level of simplification is not usually too important for welded structures, but may significantly influence fatigue life in the cases of highly irregular load histories. If level 2 simplification is justified, then level 3 simplification is also normally a good assumption. However, the lost information may be important when deciding on a suitable omission level or when assessing potentially harmful effects caused by large tensile or compressive stresses

Ted

 

[namelessudhay]

Hi Ted,

Thanks for giving the information. The piece that I miss in the reference is:

"The equivalent stress range concept in Eq. 8.4 is easily derived assuming a constant S–N slope and D = 1"

I am curious to see this part.

 

[namelessudhay]

@rb1957 - Thanks for the links. Info. in aerospaceengineering page was interesting. My objective is to know how the equation "Teq^p*sum(ni) = sum(Ti^p*ni) … " is derived.

 

[rb1957]

It seems to be a reasonable engineering approximation, it's like a weighted average.

Why are you looking for a derivation of an equation in the standard ? for your own education/enlightenment ? or because you've a similar situation and you're looking to extrapolate this application to your example ?

Doesn't the standard refer to a source ? Aren't there textbooks in the field that'd help ?

another day in paradise, or is paradise one day closer ?

 

[namelessudhay]

@rb1957 - The purpose is a bit longer and complex to explain in the post here. Long story short - I used a more derived method to find the damage in a shaft. When my colleague used the ISO standard referred Palgmer-Miner's method he found a different damage value. I wanted to know where exactly does the difference begin.

 

[rb1957]

did you use the same "p" exponent ?

the equation is very typical. essentially saying that life (N) is proportional to L^p (p is negative, right) and damage is (by Miner's rule) n/N. The RHS of the equation is summing each of the load levels, the LHS is saying there is one "equivalent" load.

Look into the details of your colleague's analysis and you'll probably see some differences in assumptions.

how does the "the ISO standard referred Palgmer-Miner's method" differ from the original equation ?

another day in paradise, or is paradise one day closer ?

 

[hydtools]

https://books.google.com/books?id=D...&q=palmgren-miner equation derivation&f=false

The Palmgre-Miner equation derives from equating experimental stress energies to prediction stress energies. The product of stress x cycles would be energy.

Ted

 

[chicopee]

Please see attachment of method used by Palgmer-Miner

 

[rb1957]

you dropped the index "p" to Ti in the last line ...

another day in paradise, or is paradise one day closer ?

 

[chicopee]

Yeah, I see it; thanks! Sometimes it is easy to omit a superscript when you have a bad cold.