Does anyone know of software that will calculate the plastic moment of resistance of a steel beam with welded Tee section at the bottom? I started writing a spreadsheet, but is a little laborious to cover all cases because the PNA can fall above the bottom flange of the beam, below the bottom flange of the beam or within the bottom flange of the beam.
Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations JAE on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Plastic Moment of resistance of beam with welded tee at bottom 2
- Thread starter ajk1
- Start date
- Thread starter
- #21
- Thread starter
- #24
But it is trial and error, and depends somewhat where the PNA is, above, within or below the beam bottom flange. In my case, it is within the bottom flange, but with the trial tee that I started with, it was above the bottom flange. So is a bit time consuming, to try several tees, compared to just picking Mr or Z out of a table as for the usual beam. I thought this was something that someone would have written a good spreadsheet for, as I have now done, although it is not that good it still saves time. But if you use the shortcut that you suggested the issue of where the PNA falls does not arise. I am not that great at doing a lot of arithmetic without mistake, so I like software, but I know some people are really good at it and would be happy doing it by hand, so I take your point.
- Thread starter
- #26
canwesteng
Structural
@BA - enough weld to develop the yield strength of the T seems pretty wasteful. Going through the shear flow calc is more than justified to figure out how much weld is required would save your client money + erection time in this case imo.
- Thread starter
- #28
canwesteng
Structural
I disagree - really you could have no weld at all at the point of zero shear, with more weld required at the ends. I don't think the fact you use plastic moment makes a difference.
canwesteng, you really ought to read my post a little more carefully. You can have no weld at any point in the span, but the total weld between the end of the tee and the point where you are relying on the plastic section must develop As.Fy. That is all I have been saying and it is irrefutable.canwest said:
BA
canwesteng
Structural
Ok, agreed you need enough weld to develop the T. I think that in virtually every case this will require less than a complete pen weld though, you just need to determine the shear on the weld.
Further thoughts.
- If you'll be plastifying the reinforcing, then it needs to be developed for Fy between the point of max moment and the end of the member. For this, one can utilize the termination welds and all of the stitch welding in between. As such, this isn't usually too onerous to satisfy.
- If the reinforcement doesn't extend full length, then it needs to be developed past the theoretical cutoff point for the amount of force assumed in the reinforcement at that point. This is MQ/I if you're elastic, As*Fy if you're plastic, or something a little fancier if you're partially plastic and feeling ambitious. It's rare for the termination welds to require As*Fy development in my experience.
- I don't think that VQ/I is technically valid for locations where the section moment exceeds the first yield moment.
- For ajk1's situation, I see no demand based justification for full pen welding. Which isn't to say that we won't do it anyhow for other reasons.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
- If you'll be plastifying the reinforcing, then it needs to be developed for Fy between the point of max moment and the end of the member. For this, one can utilize the termination welds and all of the stitch welding in between. As such, this isn't usually too onerous to satisfy.
- If the reinforcement doesn't extend full length, then it needs to be developed past the theoretical cutoff point for the amount of force assumed in the reinforcement at that point. This is MQ/I if you're elastic, As*Fy if you're plastic, or something a little fancier if you're partially plastic and feeling ambitious. It's rare for the termination welds to require As*Fy development in my experience.
- I don't think that VQ/I is technically valid for locations where the section moment exceeds the first yield moment.
- For ajk1's situation, I see no demand based justification for full pen welding. Which isn't to say that we won't do it anyhow for other reasons.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
canwesteng
Structural
I disagree with needing As*Fy for the welds. VQ/I isn't valid but you should still calculate shear flow between the parts based on your assumed stress distribution. See the response to the question here in steel interchange
- Thread starter
- #35
The penetration welding was because there is access from one side only, so I was going to weld a backer bar at intervals on the tee stem before lifting the tee stem into place . There is a parallel block wall located about 2" to the south of the beam flange. I don't think it would be ok to just fillet weld one side (the accessible side) of the new tee stem to the bottom of the existing beam....or would it (although it would simplify things)?
canwesteng
Structural
No, fillet welding only side would be a very poor detail, I got quite sidetracked. Maybe stitch CJP if possible? This takes a hand calc to figure out though, not aware of any software that will work it out for you.
- Thread starter
- #37
A full penetration weld is required for symmetry as pointed out by ajk1 but it does not need to be continuous; in fact it likely will not be continuous as that would be excessive.
Using the relationship VQ/I for shear flow may be adequate for the present case. I don't know as I haven't checked it. But one cannot disagree with needing a total of As*Fy at each end of the tee. How else is the tension going to get into the tee other than by the weld under discussion?
BA
Using the relationship VQ/I for shear flow may be adequate for the present case. I don't know as I haven't checked it. But one cannot disagree with needing a total of As*Fy at each end of the tee. How else is the tension going to get into the tee other than by the weld under discussion?
BA
canwest said:
Thank you for posting this canwest. While I'd never attempted to calculate the plastic version of VQ/I, I must confess that I was one of those folks who erroneously assumed that it would be greater than VQ/I. It's good to know the truth of the matter.
BAretired said:
I agree with this as well although, for the sake of precision, I'd tweak it to "a total of As*Fy
@BA: just realized that you provide a more precise version of your statement previously. My bad. It was:
BAretired said:
Try this on for size:
In these scenarios, we design our welds to satisfy two requirements:
1) We design our intermittent/continuous welds to deal with the increment of moment at each location. This is the VQ/I stuff for elastic situations and the analogous formulation for plastic situations.
2) We design our intermittent welds and termination welds such that, when taken together, they are capable of developing the entire force delivered to the reinforcing at the point of maximum moment.
Additional observations:
1) When reinforcement extends the full length of the original member, termination welds are technically not required.
2) When reinforcement extends only partial length, the VQ/I welds (set out precisely and varying) will not adequately resist the entire force delivered to the reinforcing at the point of maximum moment. Additional termination welds are required to make up the deficiency. These are the MQ/I welds or the analogous formulation for plastic situations (often conservatively taken as As x Fy).
I've attempted to summarize all this graphically below.
In the document that canwest supplied above, Mr. Muir presents the equation shown below for the shear flow in an elastic wide flange. I believe it to be in error and feel that the expression should be multiplied by d/2. That doesn't change any of the conclusions developed in the document however.
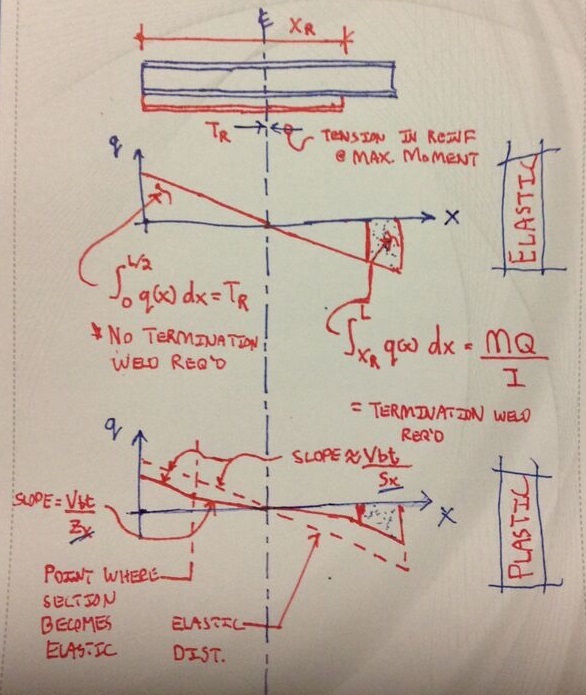
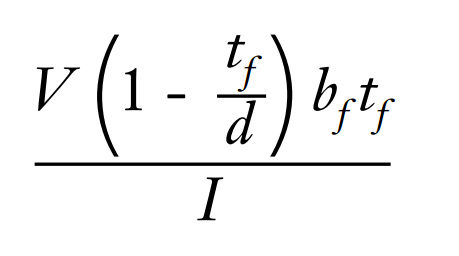
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.
It seems to make sense to determine the total length of full penetration weld required to resist As.Fy of the tee, then to provide that length in an intermittent weld with weld segments spaced equally each side of the maximum moment (assuming uniform load). To be on the safe side, I would add a double length of weld at the extreme ends of the tee.
BA
BA
- Status
Similar threads
- Question
