Post Tension - Fundamental Theory

[Fevola]

Hi All,

Very new to PT design. I have been reading bits and pieces of theory. I understand P/A, I understand P applied at at distance E from the centroid is P.e. I've read about equivalent load... GREAT.

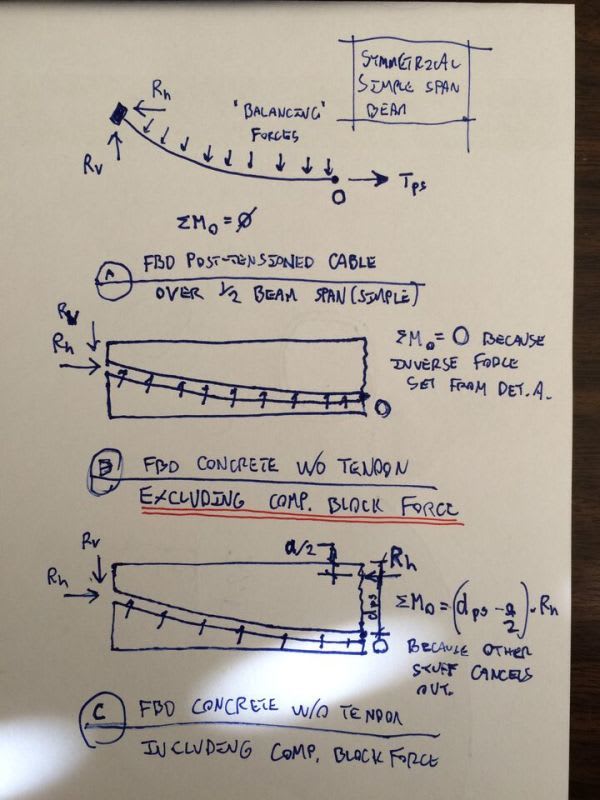
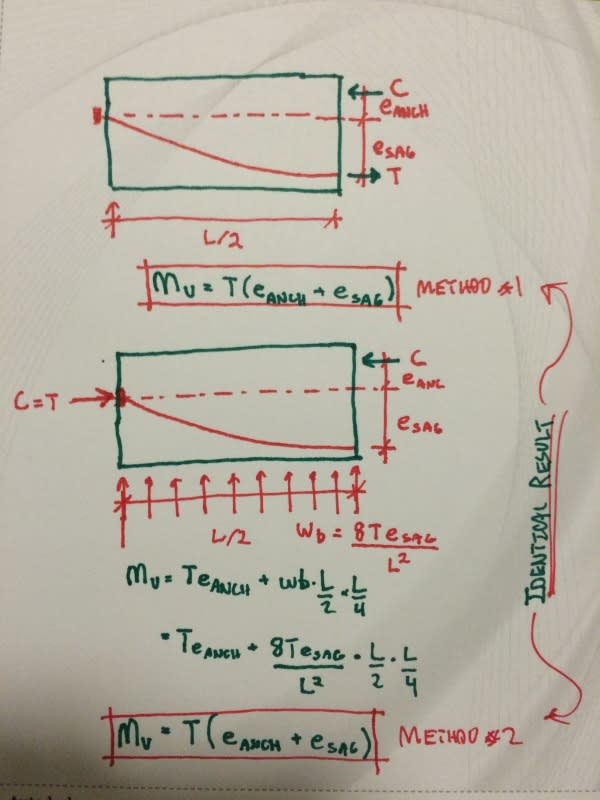
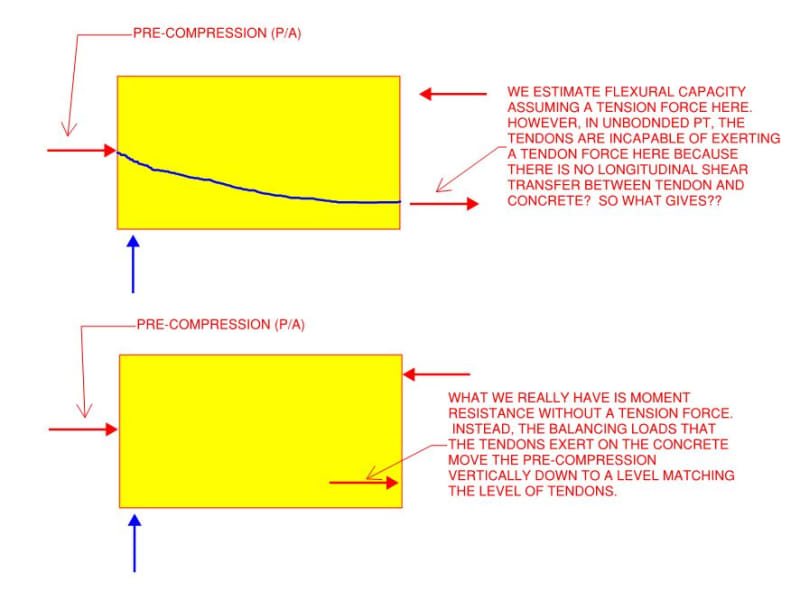
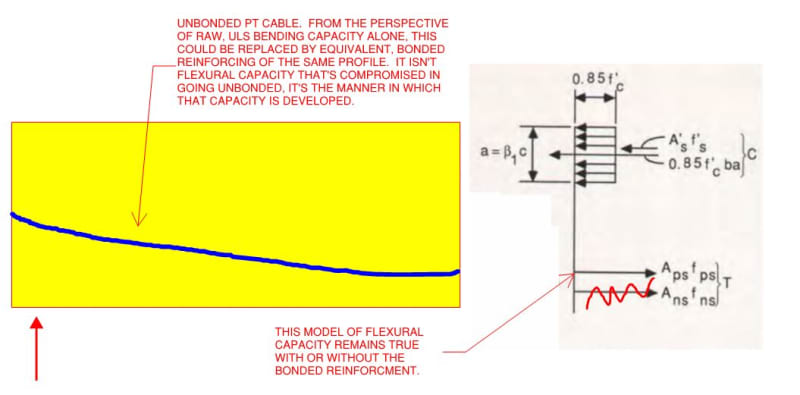
In order to properly I understand this, I feel I need to go back further into basics and fully understand the unbonded situation. Stressing tendons and then anchoring them at the ends of a beam/slab applies a compressive force (P/A) throughout the length of member. If the anchorage lies above/below the member centroid, there is also a moment applied to the end of the beam. The bit that confuses me is, without grouting, how can there be a transfer of force between tendon and concrete, other than at the end anchorage zones as mentioned above. The only other way I can visualise force being transferred is through catenary action when a draped tendon tries to straighten under applied tension loading - I believe the tendancy of the tendon to straighten is what lifts the beam/slab (or counteracts the applied vertical loads). But nobody ever seems to mention catenary action so I am obviously missing something.
Without bonding the tendons, and neglecting catenary action, I also do not see how the profile/drape plays any part - all that matters is what happens at the anchorage zone because there is no force interaction between tendon and concrete anywhere else.

 

[3DDave]

If a moment causes a differential in tension/compression between two sides of a beam then the converse is also true - a differential in tension/compression between two sides of a beam causes a moment.

Consider an archery bow - the string doesn't pass through the wood of the bow and only contacts at the ends, but there is a bending moment through the wood.

Perhaps the way it is phrased is odd?

 

[Celt83]

Here are two threads:
my own thread where I had the same hang up: Link
One Where Rapt, KootK and others go through a similar discussion: Link


My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[KootK]

1) You're spot on with respect to your understanding. Excluding local effects, the forces that you mentioned are all that the tendons will exert on the concrete: the anchorage forces and the load balancing forces (curvature / straightening). I examined this myself in the first sketch below, taken from the thread that Celt83 referenced.

2) The first sketch below is one that I created for the thread that Celt93 referenced. In it, I demonstrated to myself that [P*e] is equivalent to load balancing.

3) I prepared the third sketch below just for this thread. In it, I consider an epiphany that I had subsequent to the other threads: it is the load balancing effect of the tendon curvature that moves the pre-compression force vertically to the level of the tendons. This is what allow us to calculate flexural capacity by treating the tendons as a tensile force on the concrete as we would with bonded reinforcement even though the tendons are not bonded. This may be obvious to others but is something that I put together fairly late in my unbonded PT career. This is really just a matter of perspective and whether one turns their attention to:

a) the concrete alone with the tendon actions superimposed upon it or;

b) the combined body including both the concrete and the tendons, even though the two are non-composite in PT.

 

[rapt]

Fevola,

What you are worring about is correct. There is only catenary action, if there is no bond. That is why ACI318 requires a minimum amount of bonded reinforcement in unbonded prestressed members, Ast = .004Act. This has been shown in tests to be sufficient to allow the member to work in flexure rather than catenary action.

 

[KootK]

@rapt: I'd like to clarify a couple of your comments. Please review the following and let me know if we're on the same page. Note that, while I don't love the term "catenary" for PT balancing forces, I'm going to continue with that nomenclature in order to remain consistent with the previous comments.

There is only catenary action, if there is no bond.

With regard to contributions to flexural resistance, there is not just catenary action but rather:

1) Catenary action AND;

2) The effect of member pre-compression.

That, unless you're considering the pre-compression to be a part of the catenary action I suppose.

This has been shown in tests to be sufficient to allow the member to work in flexure rather than catenary action.

While the bonded reinforcement will augment capacity and encourage a more conventional, flexural behavior at ULS, it will not generally replace the bending resistance generated by the tendon drape. The catenary action is still a primary source of ULS flexural resistance, with or without the [0.004 x Act].

 

[rapt]

Kootk,

I was referring to the ultimate failure mode of the member if there is zero bonded reinforcement, not the calculation of or effect of balancing forces. There would be one very large crack and it would essentially become a cable structure. There would be no flexural action. It would be supported by a cable element in catenary action.

By adding the minimum bonded reinforcement required by ACI, it was found that the member acted like a flexural member with multiple cracks and C = Tp + Ts providing a moment couple like any normal flexural member.

It then becomes interesting with a segmental box girder bridge with external unbonded tendons and no continuous reinforcement. It can never fail as a flexural member so must be kept in compression under all load conditions.

 

[KootK]

Thanks for the response rapt. I looked into the paper that was the source doc for the [0.004 x Act], shown below. It seems to me that the bonded reinforcement is little more than a nod towards improved crack control -- size and distribution -- and the positive things that does for ductility and serviceability. Check.

C = Tp + Ts providing a moment couple like any normal flexural member.

I feel that it's still a bit different from a normal flexural member in that the catenary action is baked into the [Tp] term. In unbonded PT, there is no physical [Tp] acting on the concrete of any particular member cross section. Rather, [Tp] is a convenient way to express the effect of the pre-compression force which has been lowered from the centroid of the member (or wherever it started off) by the catenary action. So [Tp] and the catenary action travel together like conjoined twins.

Consider two cases, each having the same, total bending capacity:

CASE 1: Unbonded PT with No Supplemental Bonded Reinforcing

You have two sources of bending resistance:

1) the catenary action, forming one part of [Tp].

2) the pre-compression, forming the other part of [Tp].

CASE 2: Unbonded PT with Supplemental Bonded Reinforcing

You have three sources of bending resistance:

1) the catenary action, forming one part of [Tp].

2) the pre-compression, forming the other part of [Tp].

3) the unboned reinforcing, forming [Ts].

Since the catenary action is present in both scenarios, I think that it's fair to say that an unbonded PT beam is, in part, a cable supported structure whether the bonded reinforcement is added or not. With the bonded reinforcement, the role of the catenary action is simply reduced with the deficit transferred to the bonded reinforcing. I see the result as essentially a cable supported structure superimposed over a conventional flexural member.

If I'm right about this, I'm surely just telling you stuff that you already know. I get that. I do so only to provoke a response should you disagree with me on any of this. That way, we can iron out our differences and I can learn from the experience.

 

[BAretired]

T. Y. Lin would be turning over in his grave if he read some of the comments in this thread.

I was referring to the ultimate failure mode of the member if there is zero bonded reinforcement, not the calculation of or effect of balancing forces. There would be one very large crack and it would essentially become a cable structure. There would be no flexural action. It would be supported by a cable element in catenary action.

While I do not agree with the widespread use of unbonded reinforcement in North America, it is for reasons other than given above. Of course there is flexural action, even without bonded reinforcement. T. Y. Lin makes this quite clear in his book entitled "Prestressed Concrete Structures" copyright 1955 by John Wiley & Sons Inc.

BA

 

[KootK]

T. Y. Lin makes this quite clear in his book entitled "Prestressed Concrete Structures" copyright 1955 by John Wiley & Sons Inc.

Any chance you'd know where in Lin's book? I've got that and would like to check it out.

Of course there is flexural action, even without bonded reinforcement.

I suspect that this might just be a semantics thing. The language choices in the Mattock article, and in the ACI commentary, are a bit strange in my opinion.

I also take it as self evident that unbonded tendons, on their own, provide flexural capacity. In the paper and the ACI commentary, they seem to equate "flexural action" with:

1) Small and distributed cracking and;

2) A ductile failure at the peak moment location.

It seems that one can successfully get those things from an unbonded PT beam when part of the flexural resistance is provided by bonded reinforcement.

 

[BAretired]

KootK,

My copy is the first edition, where this issue is treated very near the beginning of the book; specifically Article 1-2 "General Principles of Prestressed Concrete".



BA

 

[rapt]

BARetired,

Yes there is flexural action, until the concrete cracks. Once it cracks, can you please let me know how there continues to be flexural action, especially as loading increases and it approaches its collapse condition without any bonded steel at the tension face?

That is not flexural action, it is a cable in catenary.

 

[Ingenuity]

Depending on the L/D ratio of the element - and the tendon arrangement - an element with only UNbonded PT (only) can be considered to primarily behave as a tied-arch with UNbonded prestressed reinforcement acting as the tension tie and the concrete as the compressive chord of the arch.

 

[BAretired]

A cable acting as a catenary resists a moment proportional to its sag, s. Mmax = H*s where H is the horizontal component of the cable tension. The force H and the vertical reactions must be supplied by external supports.

A cable in a simple beam is anchored at each end of the beam at the neutral axis, so the force H is carried by concrete in compression. The cable has a sag, s, and at midspan, the tension, H is applied at 's' below the neutral axis. The compressive force, C is equal in magnitude to H, and is located above the neutral axis by a distance 'a', greater than zero. The distance between C and H, or the moment arm, is s+a. The moment developed at midspan is C(s+a) or H(s+a).

At any position in the span, 's' and 'a' can be determined as can 'C' and 'H'. I call that flexural action. It applies, even after the concrete cracks, although tensile stress is limited by code. Flexural action is clearly much more than "a cable in catenary".

BA

 

[rapt]

Read R9.6.2.3 in ACI318-2014, which references the Mattock paper and suggests that the minimum bonded reinforcement is required to ensure flexural behavior after cracking, otherwise you get tied arch behavior (their words). Flexural behavior requires bond between steel and concrete at the crack to provide a tension tie across the crack. Otherwise as the crack opens, the the only connection between the concrete and the tension force is at the anchorages. That is not flexural behavior.

The performance of a simply supported unbonded member with no bonded reinforcement as load increases would be (thanks Ingenuity for the list below)

1. initial flexural behavior
2. midspan, wide flexural tension crack;
3. tied-arch behavior;
4. compression crushing in concrete;
5. followed by catenary action.

Once you reach stage 3 Tied arch behavior, there are 3 possible collapse modes, concrete compression failure, steel tension failure, anchorage failure.

If compression failure occurs, which is most likely, it then becomes a Catenary mode, and yes, the horizontal component of the cable force then must be taken by the external supports.

If you get wedge slip at the anchorages or anchorage failure, you no longer have a structure.

 

[BAretired]

Found it, rapt! I was not aware of that article in the code (see below), but I won't argue the point, even though I can't say I understand it. It seems to be based on research comparing bonded to unbonded beams and was likely not contemplated in the early works of T. Y. Lin, but I could be mistaken about that too.

BA

 

[BAretired]

BA[/color]]Once you reach stage 3 Tied arch behavior, there are 3 possible collapse modes, concrete compression failure, steel tension failure, anchorage failure.
I would have expected those three modes. They are similar to failure of a reinforced concrete beam with the exception of anchorage failure, the possibility of which is one of the reasons why I don't like unbonded PT; however it is not remedied by providing As,min = 0.004Act.

If compression failure occurs, which is most likely, it then becomes a Catenary mode, and yes, the horizontal component of the cable force then must be taken by the external supports.
It is extremely unlikely that external supports would be capable of taking such a force. I would agree that compression failure is a collapse condition, but that is equally true for conventionally reinforced beams.

If you get wedge slip at the anchorages or anchorage failure, you no longer have a structure.
Anchorage failure, as mentioned above, is a concern with unbonded systems.

BA

 

[KootK]

...even though I can't say I understand it.

I really do think that the confusion here is just semantic confusion related to the poorly defined term "flexural behavior".

All that you and I have been saying (I think) is that, per the sketch below, unbonded tendons will produce flexural resistance at all locations whether there's bonded reinforcement in the mix or not. And I doubt that anybody here disputes that. What changes with the addition of bonded reinforcement is simply the manner in which flexural resistance is developed. It's character.

I feel that this substitution would go a long way towards clearing up the confusion on this:

ACI/Mattock Phrasing: "Flexural Behavior"

Improved Phrasing: "A flexural response characterized by continuous curvature (Bernoulli flexure) rather than abrupt curvature discontinuities (big cracks / tied arch)".

Bernoulli flexure does get you some desirable stuff that tied arch behavior does not. But both are capable of developing flexural capacity.

 

[rapt]

BARetired,

The idea of the comparison as I understand it was to add sufficient bonded reinforcement to make the beam act flexurally similar to an equivalent bonded prestressed beam.

RE Compression failure,

Agreed that is a possible failure mode for members with bonded reinforcement. But we check for that and try to limit the possibility of it happening by either limiting strains or indirectly with steel ratios. Plus we add an extra factor of safety with a reduced capacity reduction factor when we are over about 70% balanced condition.

For unbonded members, we still check for it but based on the assumption of it being a flexural member. No-one I know of checks and limits it as a Tied Arch. I think you will find the compression stresses are much higher due to the much increased deflection in a tied arch. All of the ACI318 design rules are based on the assumption that it is acting as a flexural member under the ultimate collapse condition

The anchorage problem is the main reason why I am against unbonded. Wedge slip definitely occurs over time in many cases (Ingenuity might like to comment on that as it is his area and he can possibly cite cases).

RE texts, I have Lin 2nd edition, but I would be reading Leonhardt or Guyon on topics like this.

 

[KootK]

...or Guyon on topics like this.

You like the 1953 single volume or the 1974 two volume?