Pressure Differential

[SMatty80]

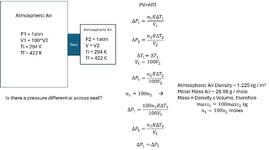
If I have two volumes with a seal in-between, both initially at atmospheric pressure and ambient temperature, will there be a pressure differential across the seal when both volumes are heated up simultaneously to the same temperature? Are the ideal gas assumptions in the example below correct in that there will not be a pressure differential across the seal? Thanks.

 

[Compositepro]

P and delta P will be the same for both volumes, although smaller masses tend to heat-up more quickly.

 

[dvd]

How does one heat these to stay at the same temperature during the heating cycle? Is the ambient surrounding environment warming up? It looks like under most circumstances that V2 will heat more quickly and thus there would be a transient pressure differential between V1 and V2.

 

[SMatty80]

Thank you for your responses! Yes the surrounding environment will be gradually heating up, so there will most likely be a small pressure differential until the two volumes reach thermal equilibrium.

 

[A8yssUK]

Now accurate do you need this? Also what pressures/dT ... will everything remain gaseous ?
Atmospheric air ?? Where and when did you sample it ? Any water content of the air ? Pollutants ? Pollen ?
Heat absorption/dissipation with the larger areas on the big volume....
Adsorption rate of the air molecules on the container surfaces...
Permeation rates through the container or through the seal or through any joins/welds ?

The seal will leak across its surfaces a little too and since there is more % seal length wrt volume with the smaller volume the smaller volume will lose more pressure during heating up.(We are talking a few 100Pa's at most) so will be a marginally lower pressure at thermal equilibrium due to there being less %mol in the smaller volume now. This differential will then drive a leak from one volume to the other...

I love how simple problems like these become really complicated when you start thinking too much about them...

 

[Taicho567]

P= (nRT) / V

The bigger the volume, the smaller the pressure, provided the n R T are constant. So there would be a dP.

 

[vhp 16 TSTC]

You start by referring to Boyle and Gai-Lussac, which is correct for any ideal gas. The problem to be solved is the change in pressure due to the increased temperature, the Volume V1 does not change. The Boyle Gay-Lussac equation can be simplified. P/T=Constant
The equation which can be used is P1 /Ti = P1" / Tf {make sure to use Kelvin temperatures!}. This should give the pressure P1” due to the temperature increase. The same goes for P2” due to the same temperature increase. The volume V1 and V2 are not part of this equation.
Ergo Conclusio. The same temperature increase on both sides of the seal give the same pressure increase.