AFG03082015
Mechanical
- Jul 14, 2016
- 26
Hello Prex, TGS4 and anyone else who may be able help!
From reading several other posts you both seem highly informed when it comes to stress linearization and was hoping you could help me out a little...
I am completing an FEA analysis to support an ASME VIII Div.1 vessel by completing the analysis to ASME VIII Div.2.
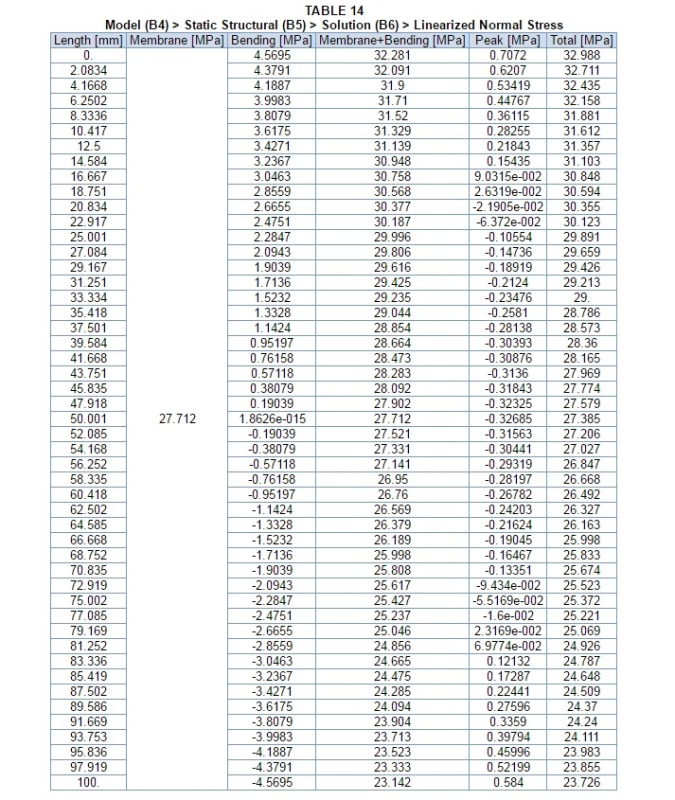
I have attached screenshots that show my 1/4 model and also the location of my SCL (The highlighted line in the centre of the three)
I have also attached the results file stating the six component stresses at each node's location along the SCL.
Would either of you be able to enlighten me as to how to proceed to calculate the Membrane Stress & Membrane + Bending Stress?
Any help would be greatly appreciated,
Thanks for your time...
From reading several other posts you both seem highly informed when it comes to stress linearization and was hoping you could help me out a little...
I am completing an FEA analysis to support an ASME VIII Div.1 vessel by completing the analysis to ASME VIII Div.2.
I have attached screenshots that show my 1/4 model and also the location of my SCL (The highlighted line in the centre of the three)
I have also attached the results file stating the six component stresses at each node's location along the SCL.
Would either of you be able to enlighten me as to how to proceed to calculate the Membrane Stress & Membrane + Bending Stress?
Any help would be greatly appreciated,
Thanks for your time...