Problem when seeking for reactions of a quite simple problem 3

[eli28]

hello,
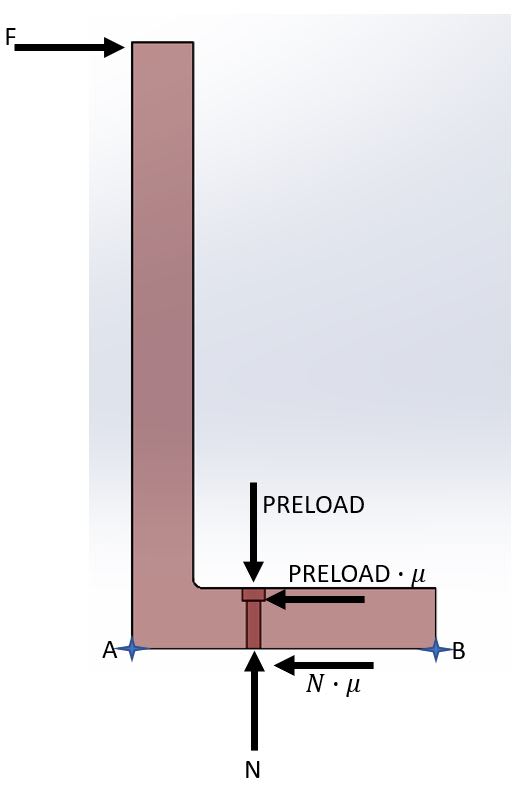
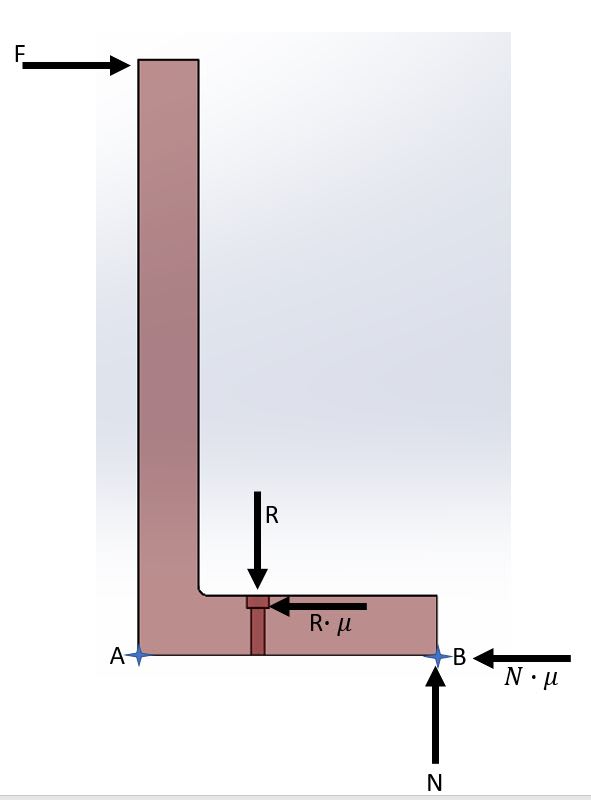
I am trying to figure out what's wrong with a free body diagram I wrote down.
I added a pdf file with a description of the problem.

please give your advice

Thanks

 

[handleman]

If I read the question correctly, we're looking at failure here, not necessarily calculating the distributed load at some arbitrary values of F. Actual mechanism of failure (assuming the no-slip condition) is the tensile failure of the bolt. Unless the bolt is severely overtorqued, the entire bottom face of the angle will lift off the surface prior to the bolt's failure. Therefore N (again, at failure condition) is acting only at the far edge.

 

[hydtools]

Once the reacting force at the bolt reaches the bolt preload there is no longer a friction-causing normal force N. There is a reaction force at the right hand edge, but it is not N. The OP defines N as the reaction to the bolt preload.

Ted

 

[desertfox]

Hi

I am late to the party but I for one wouldn’t use a single bolt in my opinion you should use at least two bolts to prevent the part rotating.

Relating to the analysis I would assume the angle was rigid and take moments about point B on the diagrams posted above, I wouldn’t worry to much about friction under bolt head because you can consider that separately once you have the force in the bolts from taking moments about point B.

I assume that the bolt will be torqued once you have an idea about the force it needs to react against, that being the case then torquing a bolt is subject to an error of about 25% unless you define exact procedures followed by extensive testing which isn’t always necessary and I can’t think it is in your case but cannot be sure.
So simplify the calculation and start with the bolt as close as possible to the vertical leg of the angle this will give you the best chance of the angle not working loose.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[eli28]

hey
I am trying to summarize all of your feedback into 2 cases (analysis configurations).
If there are still some issues (hope not) - write your comments.

1. the first is while there is no separation between the surfaces - which is right as long as the bolt isn't loaded above its preload.
in this case there is probably triangular symmetrical (relative to the bolt axis) distributed normal reaction from the floor.

2. the second is while there is seperation.
in this case there will be a hinge effect and there will be theoretically one point of reaction, point B (the righr one).

 

[rb1957]

just my 2c …

in 1) … I've never seen anyone consider friction due to preload

in 1) … there has to be some distance between the fastener load and the other reaction force, N, in order to react the overturning moment due to F. The fastener load is not the preload … once F is applied and the base reacts some moment, there is an added tension load in the bolt. The preload is reacted by an opposing distributed load to the supporting ground (equal and opposite).

in 2) … I don't understand friction due to R between the fastener head and the part

in 2) … the ultimate state with a gapped flange, I'd have the reaction to F as shear on the bolt … things aren't going to come apart (or fail) until the fastener shears.

another day in paradise, or is paradise one day closer ?

 

[handleman]

I agree with 2.

1 is FAR more complicated. The force distribution in that case depends on the deformed shape of the angle as you slowly load it. I would be quite confident that it's not an evenly distributed triangle. But, that doesn't matter. Nobody cares. There is no reason to need to know the shape or evenness of the distribution unless you're going far beyond simple µN dry static friction. Only the value of the normal force amount matters.

 

[BrianE22]

Looks close - but I would not assume you are getting much friction help from the bolt head against the bracket (preload * mu). For the top of the bolt to contribute to the friction the bolt would have to be very stiff in both bending and shear.

Also, instead of "preload" in the top picture, it would actually be "bolt load" (= preload but some extra due to the applied load).

 

[handleman]

"… I've never seen anyone consider friction due to preload"

I assume you're meaning friction between the bracket and the bolt head due to preload? As opposed to friction between the bracket and base due to preload, which is the basic foundation of bolted joint design...

"the ultimate state with a gapped flange, I'd have the reaction to F as shear on the bolt … things aren't going to come apart (or fail) until the fastener shears."

Disagree... Unless the bolt is quite far away from B relative to the height at which F is applied, the bolt will never see the shear because N will be quite large. If lengths are known, you can calculate N easily by summing moments around B. If µN is > F, there will be no slipping. Therefore the bolt will really never see shear. It will fail in tension by being "pried" apart. Of course, in this diagram the friction reaction is labeled as µN. Obviously µN is the maximum available friction force. In reality, the friction force value is simply F unless F > µN, in which case there will be slippage until the bolt contacts the edge of the hole.

 

[hydtools]

You need to review how an external load is transferred to a bolt with a preload.

https://www.boltscience.com/pages/basics1.htm

1) There would be another load applied to the bolt in reaction to the overturning load F about point B. As this reaction increases in response to increasing F, more and more reaction is transferred to the bolt as the joint clamping is decreased. N also decreases with decreasing clamp load as more reaction is transferred to the bolt. There is no need to presume any form of distribution of the normal force N.

Ted

 

[desertfox]

Hi

Check this link out and look for sub-heading bolts in bending:-

https://roymech.org/Useful_Tables/Screws/Bolted_Joint.html

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein