David_HVAC_Learning
Mechanical
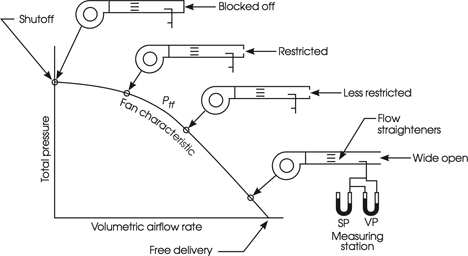
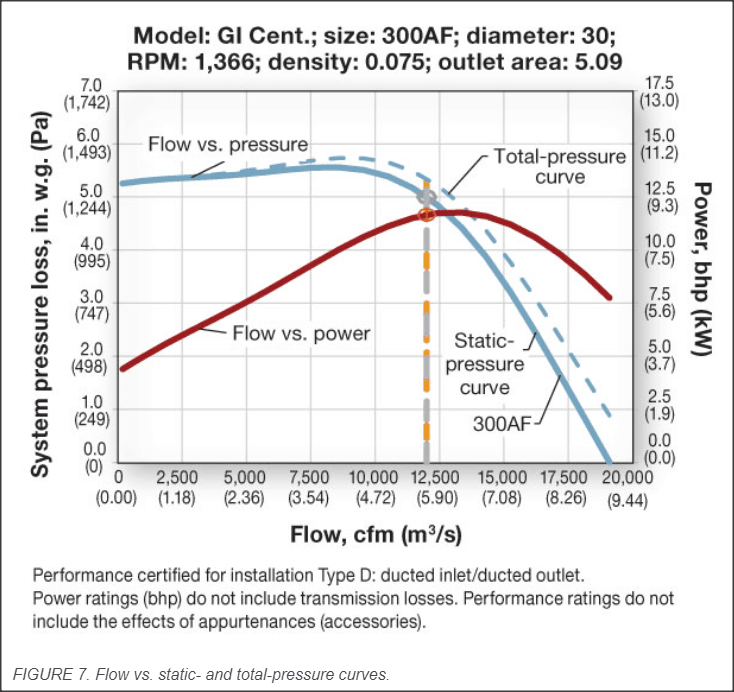
So, the above figure, is almost the same figure that is shown in the 2016 ASHRAE Handbook - HVAC Systems and Equipment (Page 21.4) with Total Pressure being defined as the fan total pressure at the outlet minus the fan total pressure at the inlet. This figure is shown in the handbook when it's discussing how a fan performance curve is obtained during testing and such. Is it correct for me to say that the reason why the total pressure (difference in pressure) on the performance curve is zero when the airflow is highest is because once the airflow reaches a certain point, the amount of friction/headloss that is produced from the fan during testing becomes equal to the positive pressure that the fan is trying to create? So in other words, they cancel out? Is my understanding correct or is there something else to it? Please let me know what you think. Thank you.