kyleShropshire
Mechanical
- May 22, 2022
- 22
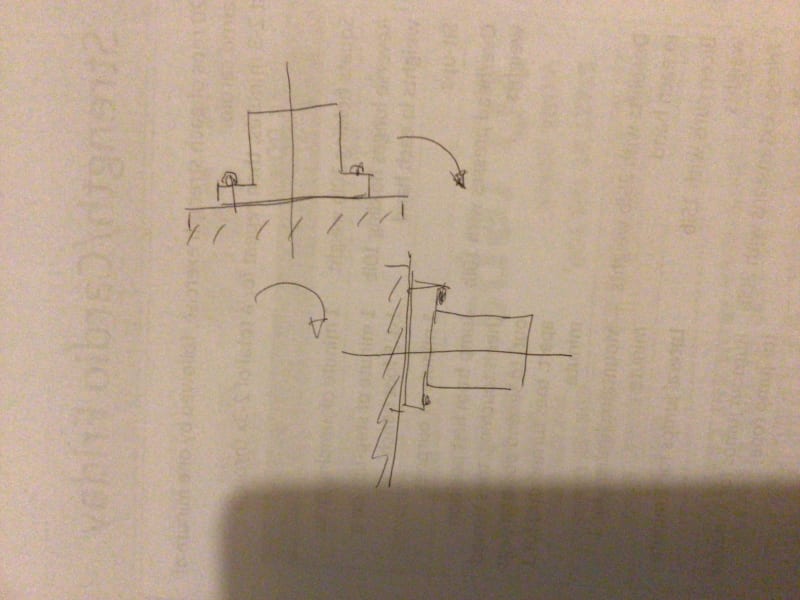
I have a cylinder rotating about its base.
When I decelerate to a stop is there a point where the ratio between the mass at the outer fibers and the center of gravity make a difference in calculating the reaction force?
The cylinder base is bolted down with four bolts and I am calculating the design factor on the bolted joint.
I was recently told this matters and want a second opinion.
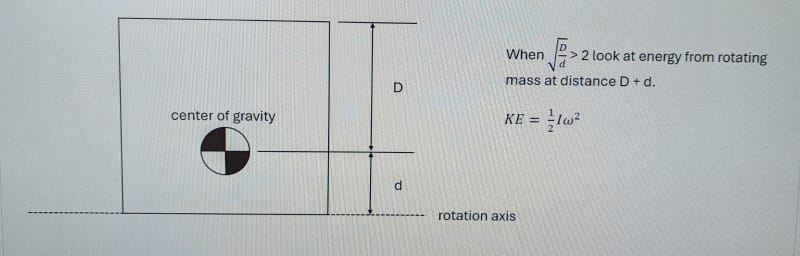
When I decelerate to a stop is there a point where the ratio between the mass at the outer fibers and the center of gravity make a difference in calculating the reaction force?
The cylinder base is bolted down with four bolts and I am calculating the design factor on the bolted joint.
I was recently told this matters and want a second opinion.