cirokos
Civil/Environmental
- Apr 11, 2022
- 63
Hello everyone,
I am running a nonlinear analysis with imperfections included by an eigenvalue buckling analysis with a factor of 0.1-0.5 ( the max dmx from buckling analysis is 1 , units are N/mm ) but the stiffness is much higher than the experimental results. How can I reduce the stiffness in order to match the experimental?
Any tips would be really helpful.
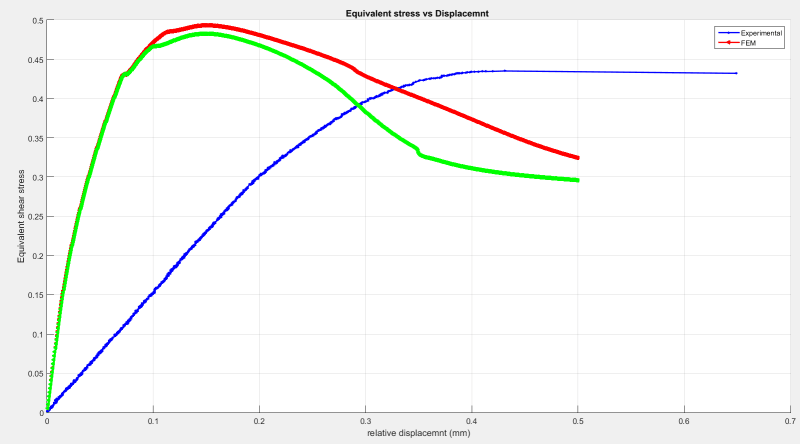
I am running a nonlinear analysis with imperfections included by an eigenvalue buckling analysis with a factor of 0.1-0.5 ( the max dmx from buckling analysis is 1 , units are N/mm ) but the stiffness is much higher than the experimental results. How can I reduce the stiffness in order to match the experimental?
Any tips would be really helpful.

