allimuthug
Civil/Environmental
Hi Everybody,
I have a channel simply supported between the columns as shown in the figure attached. The channel is connected to the column flange by a shear tab or fin plate.
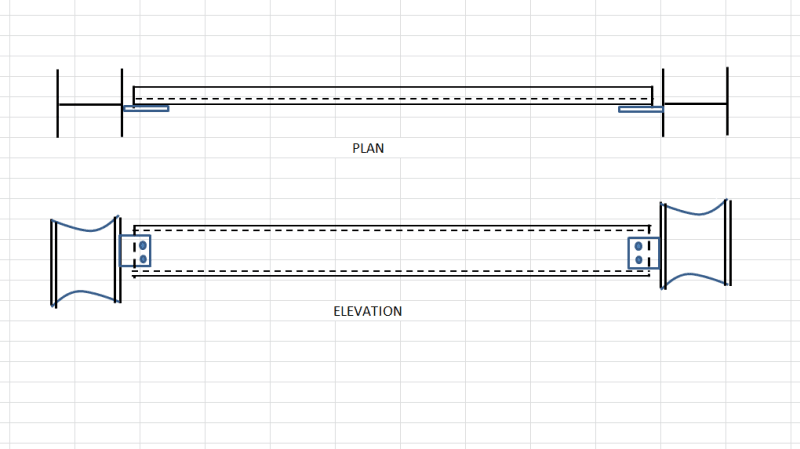
(i)As per AISC 360-05 clause F1 "The provisions in tis chapter are based on the assumption that the points of support for beams and girders are restrained against rotation about their longitudinal axis" It means the fin plate or the shear tab should be restrained against rotation or should have torsional capacity ?
(ii) It the fin plate doesn't have any torsional capacity this AISC 360 is no more applicable to the channel since it doesn't quality the assumption of AISC?
(iii) How much is the torsional rotation the fin plate is subjected to?
Please clarify me I am totally confused, because if this doesn't work then the whole world cannot use fin plate connection at all.
I have a channel simply supported between the columns as shown in the figure attached. The channel is connected to the column flange by a shear tab or fin plate.

(i)As per AISC 360-05 clause F1 "The provisions in tis chapter are based on the assumption that the points of support for beams and girders are restrained against rotation about their longitudinal axis" It means the fin plate or the shear tab should be restrained against rotation or should have torsional capacity ?
(ii) It the fin plate doesn't have any torsional capacity this AISC 360 is no more applicable to the channel since it doesn't quality the assumption of AISC?
(iii) How much is the torsional rotation the fin plate is subjected to?
Please clarify me I am totally confused, because if this doesn't work then the whole world cannot use fin plate connection at all.



