Hi,
I need to replicate a bandpass filter of which I only have the A et B coefficients (numerator and denominator of the Z-transform function). It is the blue curve in this picture.
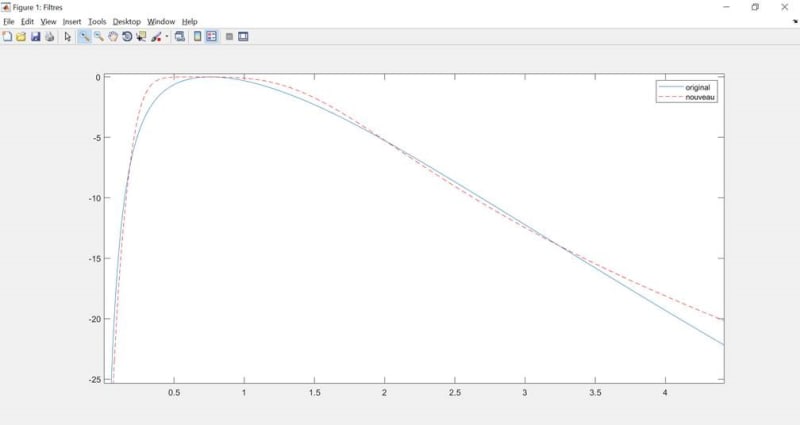
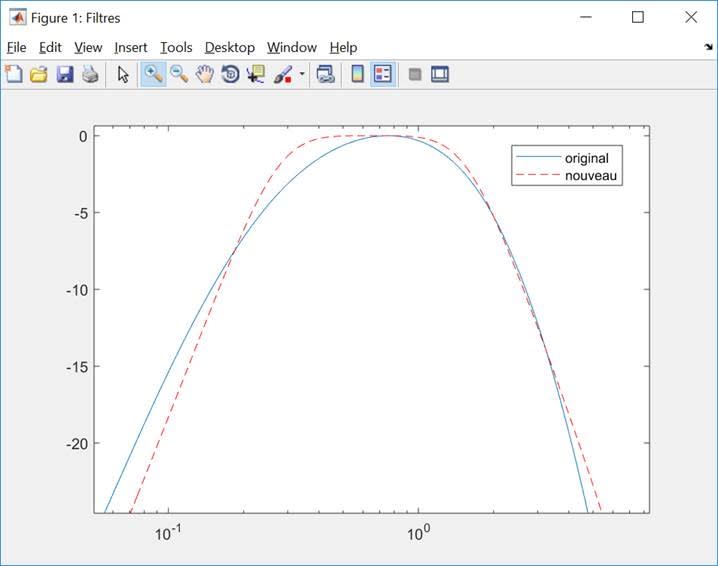
The goal is to approach this curve with my own filter, so I could eventually change the cutoff frequencies if needed, while keeping the same shape. I've tried to replicate it with a Butterworth bandpass filter (the red curve on the first picture). It is similar but not perfect. The slopes look alike but the problem is in the zone between 0.3 and 1.5 Hz. As we can see in this second picure (x axis in log), the Butterworth filter is way flatter so it doesn't filter enough around these frequencies.
Would you have any suggestion of a filter type which could approximate the filter I need to replicate (blue curve)?
Thank you!
I need to replicate a bandpass filter of which I only have the A et B coefficients (numerator and denominator of the Z-transform function). It is the blue curve in this picture.

The goal is to approach this curve with my own filter, so I could eventually change the cutoff frequencies if needed, while keeping the same shape. I've tried to replicate it with a Butterworth bandpass filter (the red curve on the first picture). It is similar but not perfect. The slopes look alike but the problem is in the zone between 0.3 and 1.5 Hz. As we can see in this second picure (x axis in log), the Butterworth filter is way flatter so it doesn't filter enough around these frequencies.

Would you have any suggestion of a filter type which could approximate the filter I need to replicate (blue curve)?
Thank you!
