Replicate a bandpass filter 1

[Jadoclou]

Hi,

I need to replicate a bandpass filter of which I only have the A et B coefficients (numerator and denominator of the Z-transform function). It is the blue curve in this picture.

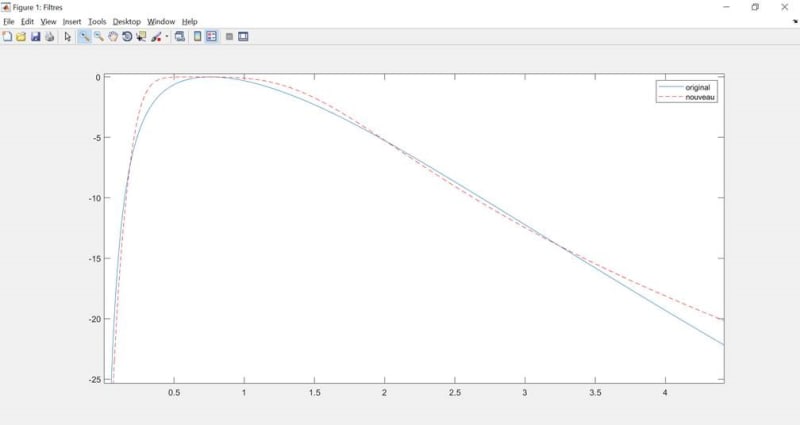
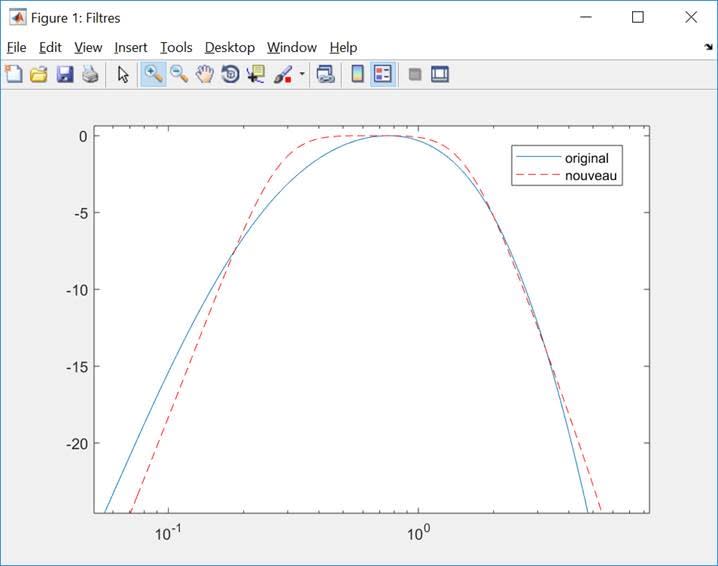
The goal is to approach this curve with my own filter, so I could eventually change the cutoff frequencies if needed, while keeping the same shape. I've tried to replicate it with a Butterworth bandpass filter (the red curve on the first picture). It is similar but not perfect. The slopes look alike but the problem is in the zone between 0.3 and 1.5 Hz. As we can see in this second picure (x axis in log), the Butterworth filter is way flatter so it doesn't filter enough around these frequencies.

Would you have any suggestion of a filter type which could approximate the filter I need to replicate (blue curve)?

Thank you!

 

[IRstuff]

Is this for school? Student posting is forbidden.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Jadoclou]

Hi,
It is not for school. I currently work in a resarch group and we are developping a wearable device which will analyse human body movements. We need to filter the collected data (like acceleration) to remove the undesirable frequencies and to reduce noise.

 

[IRstuff]

OK, but the collected data will be digital, so why not use discrete filter?

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Jadoclou]

Yes, it can be a discrete filter. It is just important that we can easily change the cutoff frequencies

 

[IRstuff]

Wouldn't the digital filter be easier to change; in addition to cut-on/cut-off, you can easily change the order of the filter?

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[VEBill]

If the OP is referring to a hardware bandpass filter, then the following perhaps applies.

These days, about the only reasons to use a hardware filter is to avoid aliasing (frequencies too high for the sampling rate), and headroom (out-of-band amplitudes too high for the ADC input, clipping).

Another reason might be to reduce digital signal processing requirements. But at these 1 Hz rates, that shouldn't be an issue.

In other words: don't filter, record everything, and extract whatever information you like from the raw data.

 

[IRstuff]

Is there an analog equivalent of the digital filter? If so, you can brute force a least squares fit the analog filter coefficients using the response curve of the digital filter, since you essentially have an infinite number of datapoints.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Jadoclou]

Yes, we could do that to replicate the blue curve, but then we would not be able to easily change the cutoff frequencies. What we liked about the Butterworth filter was that we can easily change the cutoff frequencies in the filter design. However, it is not that close to the original one. We were looking for a generic filter (butterworth, chebychev, etc.) that would look more like the blue curve and that we could then easily shift the cutoff frequencies.

 

[IRstuff]

Either way, you should still be able to get a best fit with even just specifying cutoff/cuton frequencies.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[benta]

Well, it seems to be a second-order conjugate pole bandpass filter, so why don't you plug in the second order transfer function into a graphing tool and play around with Q or damping factor? This is even easily done in Excel or other spreadsheets.