SteelCrane
Structural
- Oct 16, 2024
- 5
Can someone explain how RISA-3D calculates Plate Principal Stresses? Specifically, how does it derive σx, σy, and τxy for use in the Mohr's Circle calculations that lead to σ1, σ2, τmax, and σVon-Mises? The methodology is described here. The Plate Forces and Plate Principal Stresses for a 2.25" thick plate output by RISA-3D are:
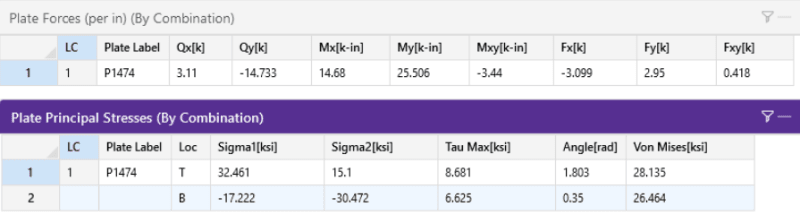
Here's what I've tried:
fax = Fx / tpl = -1.377 ksi
fay = Fy / tpl = 1.311 ksi
fbx = 6*Mx / tpl2 = 17.399 ksi (+ at top)
fby = 6*My / tpl2 = 30.229 ksi (+ at top)
fbxy (warp) = 6*Mxy / tpl2 = -4.077 ksi
fxy = Fxy / tpl = 0.186 ksi
fxz = Qx / tpl = 1.382 ksi
fyz = Qy / tpl = 6.548 ksi
Attempt #1:
σx = fax + fbx + fbxy (warp)
σy = fay + fby + fbxy (warp)
τxy = max of:
Resulting error: 17% for σ1, 17% for σ2, 17% for τmax
Attempt #2:
σx = fax + fbx
σy = fay + fby
τxy = max of:
Resulting error: 5% for σ1, -10% for σ2, 17% for τmax
Attempt #3:
σx = fax + fbx
σy = fay + fby
τxy = fxy
Resulting error: -3% for σ1, 6% for σ2, -11% for τmax
Attempt #4: at this point, I gave up and backsolved the RISA-3D Principal Stress results to find σx, σy, and τxy, and it led to this:
σx = fax + fbx (excluding warping) = 16.02 ksi
σy = fay + fby (excluding warping) = 31.54 ksi
τxy = 3.89 ksi; a number I can't derive using any combination of Fxy, Qx, and/or Qy
Resulting error: 0% for σ1, 0% for σ2, 0% for τmax
Given that fxy = 0.186 ksi, fxz = 1.382 ksi, and fyz = 6.548 ksi, how did it come up with 3.888 ksi? And why would the warping moment be excluded?
Thanks for your help!

Here's what I've tried:
fax = Fx / tpl = -1.377 ksi
fay = Fy / tpl = 1.311 ksi
fbx = 6*Mx / tpl2 = 17.399 ksi (+ at top)
fby = 6*My / tpl2 = 30.229 ksi (+ at top)
fbxy (warp) = 6*Mxy / tpl2 = -4.077 ksi
fxy = Fxy / tpl = 0.186 ksi
fxz = Qx / tpl = 1.382 ksi
fyz = Qy / tpl = 6.548 ksi
Attempt #1:
σx = fax + fbx + fbxy (warp)
σy = fay + fby + fbxy (warp)
τxy = max of:
{fxy and fxz resolved}
{fxy and fyz resolved}
Resulting error: 17% for σ1, 17% for σ2, 17% for τmax
Attempt #2:
σx = fax + fbx
σy = fay + fby
τxy = max of:
{fxy and fxz resolved}
{fxy and fyz resolved}
Resulting error: 5% for σ1, -10% for σ2, 17% for τmax
Attempt #3:
σx = fax + fbx
σy = fay + fby
τxy = fxy
Resulting error: -3% for σ1, 6% for σ2, -11% for τmax
Attempt #4: at this point, I gave up and backsolved the RISA-3D Principal Stress results to find σx, σy, and τxy, and it led to this:
σx = fax + fbx (excluding warping) = 16.02 ksi
σy = fay + fby (excluding warping) = 31.54 ksi
τxy = 3.89 ksi; a number I can't derive using any combination of Fxy, Qx, and/or Qy
Resulting error: 0% for σ1, 0% for σ2, 0% for τmax
Given that fxy = 0.186 ksi, fxz = 1.382 ksi, and fyz = 6.548 ksi, how did it come up with 3.888 ksi? And why would the warping moment be excluded?
Thanks for your help!

