Gavin_yang
Mechanical
Hi everyone, I'm trying to learn RSS in tolerance analysis these days and I just have some question, pls give me some help thx.
In RSS, we need to set a Cpk values for all parts (most common = 1.33)
I just want to know are there any assumptions or requirements that the Cpk of each parts need to be the same
Because the process capability of diffierent factories may not be the same, like Cpk(factory A)=1.33, Cpk(factory B)=1.0, Cpk(factory C)=1.33 ... something like this
So when performing tolerance analysis, could I just use diffierent Cpks for each parts in calculating ?
Dimension A → 5±0.5 Cpk=1.33
Dimension B → 2±0.3 Cpk=1.0
Dimension C → 4±0.5 Cpk=1.33
Goal X → X=A+B-C 3±T Cpk=1.33
In RSS, we need to set a Cpk values for all parts (most common = 1.33)
I just want to know are there any assumptions or requirements that the Cpk of each parts need to be the same
Because the process capability of diffierent factories may not be the same, like Cpk(factory A)=1.33, Cpk(factory B)=1.0, Cpk(factory C)=1.33 ... something like this
So when performing tolerance analysis, could I just use diffierent Cpks for each parts in calculating ?
Dimension A → 5±0.5 Cpk=1.33
Dimension B → 2±0.3 Cpk=1.0
Dimension C → 4±0.5 Cpk=1.33
Goal X → X=A+B-C 3±T Cpk=1.33

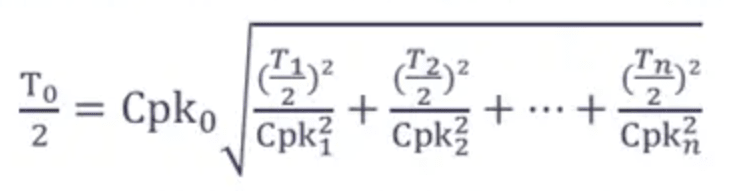
![[shriner] [shriner] [shriner]](/data/assets/smilies/shriner.gif) .
.