Shear Flow across Horizontal Construction Joint in Reinforced Concrete Beam

[BridgeEngineer21]

I have a large solid box reinforced concrete beam (h = 5m, b = 4m) with a horizontal construction joint 3.5m from the bottom. I am working with a spreadsheet previously set up by someone else that checked the situation referring to Eurocode 2, 6.2.4:

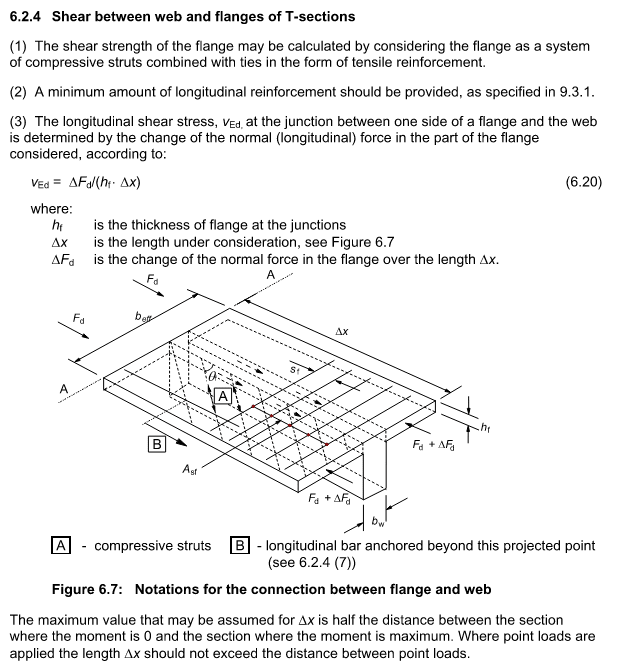
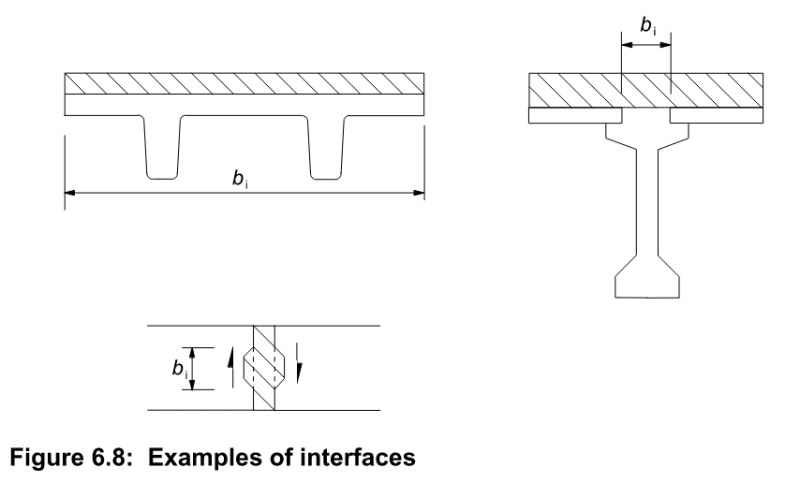
They calculated q = VQ/I, with V = vertical shear, Q = moment of area of the upper 1.5m of the beam, I = Gross moment of inertia of the full depth concrete beam. They then took vED = q/b to get the shear stress across the joint and compared that to the capacity of VRdi, which comes from 6.2.5:

My first issue is it doesn't seem to make sense to refer to 6.2.4 at all, and this whole thing would be most appropriately covered just following 6.2.5. Would be interested to hear any thoughts on that from those familiar with Eurocode.

Secondly, I'm having a doubt about the calculation of q. I know the theoretical principle but have only every applied it in practice to steel beams. Considering that I am checking ultimate loads and the beam will be cracked, using I = Ig doesn't seem appropriate, but I'm not really sure what is best. Since I want to know the actual shear flow in the concrete on both sides of the joint, it seems weird to use the cracked moment of inertia which disregards the concrete below the NA, which will likely end up above the joint. So I am looking for some advice on what I should consider for I here?

Thirdly, this beam also has a not insignificant and reversible axial force, as well as horizontal transverse shear, which can be applied at any point along the beam's height, which means there can also be torsion. (To be clear, I'm not manually calculating forces in the beam, I already have output from a 3D model with concurrent forces and moments in all three directions at 10th points along the beam). Once I get my shear flow due to vertical transverse shear, do I have to somehow add in axial force, horizontal transverse shear and torsion to get a "total" shear flow across the interface that I would then check against the interface shear capacity? The previous calculation disregarded all of these which seems wrong to me.

 

[BridgeSmith]

Then the 2h/3 would be the correct z distance for a beam of linearly elastic material. The stress and force diagram is triangular. It varies linearly from the max at the top and bottom of the beam to zero at the neutral axis. The centers of the C and T areas are at 2/3 the distance from the NA to the top and bott. Of course, in concrete, especially reinforced concrete, the stress and force distribution isn't close to being linear, and I and Q have to be calculated ignoring the concrete in tension.

 

[BridgeEngineer21]

Ah, of course, knew I was missing something. Thanks

 

[Smoulder]

@Bridgeengineer21 This isn't the right equation for vert joint with vert shear. Say you have a vert joint but the load is applied across full width of beam. Each side just carries its own load and they deflect the same so no shear on the joint. You could just have two beams. You get joint shear if the load is applied on one side only but it will be local to the load point.

 

[BridgeEngineer21]

Not sure I follow the scenario you're describing Smoulder. Are you talking about vertical joints along the longitudinal axis of the beam? I was thinking about transverse vertical joints. In the same beam I sketched above, I will have transverse vertical joints located at third points of the span. Of course, there is differential shear across those joints. So does 6.24 apply there, but with beta set to 1?

 

[Smoulder]

Gotcha. Don't think there's a check for that. Locate where shear is small if possible which sounds like you have and then it's up to construction quality. A bit of extra reo locally won't hurt to hold it all together but that's a lot of steel in your size of beam. What are you designing? Thought it might be the solid part of a box girder over pier but not if you're at the third points.

 

[BridgeEngineer21]

I would think the interface shear capacity equation (EN 6.25) should be valid regardless of joint orientation, no? In the past I've always used AASHTO 5.7.4.3 which is essentially the same equation.

If I'm thinking about it correctly, demand should be very simple, V/bz with β = 1. Just the transverse shear stress across a vertical plane.

This is a foundation beam supporting a maritime structure. There are four piles in a square formation with beams spanning between them in two directions. The governing load is ship impact which can be directly on the piles or in the beam span. Impact on the piles causes maximum moment on the beams around the perpendicular horizontal axis, while impact in the center of the beams causes maximum moment about the vertical axis (and torsion since impact can be eccentric vertically).

By the way, I think we've covered it quite well at this point, but I just noticed that AASHTO equation 5.7.4.5-1 is essentially the same as EN 6.24, just assuming β = 1. And the commentary C5.7.4.5 gives a good explanation of how that equation is derived which would have basically answered all my questions in this thread. Another reason to prefer AASHTO to Eurocode

 

[BridgeEngineer21]

Hi all - I am opening this thread back up with a new question.

I'm now pretty settled on using equation 6.25 for this purpose, after the discussion on here and some subsequent discussions with a senior engineer in the office.

Now I'm honing in on the ρ*fyd term which in the equation which is causing some problems. ρ = As/Ai with As defined as follows:

Since this is a horizontal joint, the reinforcement we need to count on is the ordinary shear reinforcement. My interpretation of the code was the full area of this reinforcement can be counted on in this equation. But the senior engineer has instructed that we should only count the portion of that reinforcement which isn't already utilized in the standard beam shear and torsion checks. Essentially, this method doubles the required shear reinforcement.

Something tells me we shouldn't be double counting the requirement like this (first designing for shear and torsion in a monolithic beam, then designing for shear and torsion across the interface, then adding the two requirements together). The vertical force transferred in these bars is just the tie force from the shear truss - doesn't that force remain the same regardless whether there is a joint or not? On the other hand, if that was the case, why would this additional check at the interface be needed at all if the beam is already designed in shear? Maybe the answer is its not needed in this case, and the check is mainly geared towards interfaces such as those pictured in Figure 6.8, between a girder and deck.

It is maybe of note that the comparable clause in AASHTO, which also is geared towards a girder/slab interface, only calls for additional reinforcement if there is net tension across the interface:

Just putting a few thoughts out loud here. I questioned it in the beginning just based on gut feeling, but my senior seemed pretty certain. I'll revisit it with him again with some more fully formed thoughts, but would be interested to hear some other opinions from you all on here.