Shear Span 2

[StructuralAddict]

I appreciate if someone can give me an answer to this:
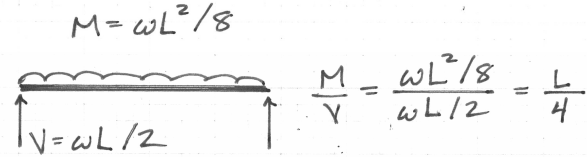
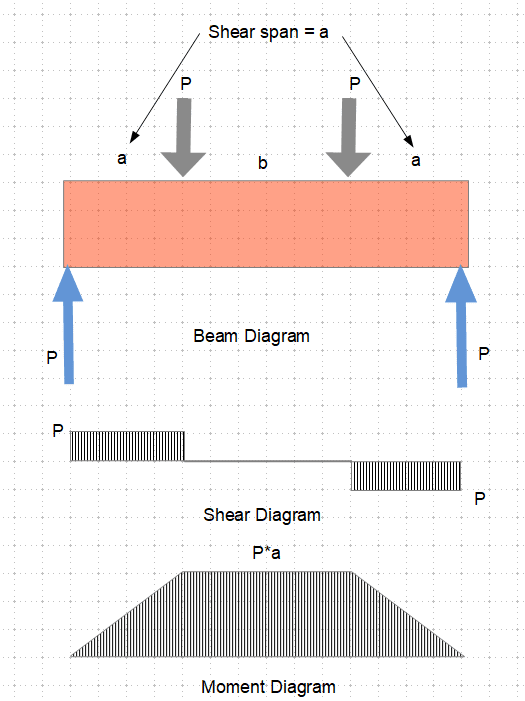
What is the shear span (M/V) of the following members?
1- uniformly loaded simply supported beam
2- cantilever with concentrated load at its tip
3- two-span continuous beam with uniformly distributed load on both spans

Thank you!

 

[r13]

StructuralAddict,

The code you use must have explanation for the terms "M/V", and "Shear Span". Can you provide it for information?

 

[Settingsun]

Fvm = 0.5[4.0-1.75(M/(V.dv))].sqrt(f'm)+0.25(P/An)

The M/(V*dv) term gives an increased shear strength near an exterior simple support similar to concrete. I assume it comes with the same condition that the load causes diagonal compression, eg not a hanger support.

It doesn't look as though you get the same benefit at a continuous support unless negative moment is taken as numerically negative (ie not absolute value) or zero. Is there explanation of that aspect?

Are there upper and lower limits on Fvm?

 

[StructuralAddict]

steveh49: Yes, there is a limit on the [M/(V*dv)] term that it is <= 1.0.

 

[StructuralAddict]

BAretired: The expression is given in TMS402/ACI530 (Building Code Requirements for Masonry Structures) and TMS602/ACI530 (Specification for Masonry Structures).

 

[StructuralAddict]

retired13: I will dig into the code for any explanation and let you know..

 

[KootK]

I believe the definition of shear span is confusing.

Clearly.

Call it M/V if you wish, but it is certainly not the shear span.

M/(V*dv) is referred to as the shear span ratio in the literature wherein M/V represents the specific, reference shear span condition shown below. That reference shear span is compared to the shear depth of the section (dv) as a way of assessing the impact of flexural stresses on shear capacity at the cross section being studied.

I suspect that the referenced shear span condition shown below was the literal shear span condition used in the lab when the testing was being done that later formed the basis of these provisions. That may be how the confusing terminology crept in.

 

[phamENG]

KootK - just to restate it to make sure I'm picking up what your putting down:

Given an arbitrary loading, you can divide the internal moment by the shear at any point in the cross section to determine an equivalent point loaded condition that would have a "true" shear span in which the shear is constant over the length e=M/V. That equivalency is what allows us to compare it to the shear depth for the determination of the available shear strength.

Sound about right? I admit I haven't dug deeply into the meaning of that term before.

 

[RPMG]

M/Vd is a unitless expression like KL/r. It is intended to be computed.

If shear span, defined as M/V, is analogous to effective length, KL, then the shear span of a simply supported beam is L/4.

If it is to be defined as length of uniform shear, then it has no relevance because it is not useful, even if that's what Quora.com says.

 

[phamENG]

Whoa. You're saying we can't trust Quora.com!? What's next? I guess you'll tell me I can't rely on getting news from the Onion anymore either...

 

[r13]

Anybody has a copy of TMS602 or ACI530, and bother to look up for the meaning of so called "shear span" in its context, and the application and implication? Thanks.

 

[StructuralAddict]

Ok, so TMS says the following:

"The provisions of this Section were developed through the study of and calibrated to cantilevered shear walls. The ratio M/(Vdv), can be difficult to interpret or apply consistently for other conditions such as for a uniformly loaded, simply supported beam. Concurrent values of M and Vdv must be considered at appropriate locations along shear members,
such as beams, to determine the critical M/(Vdv) ratio. To simplify the analytical process, designers are permitted to use M/(Vdv) = 1. Commentary Section 9.3.4.1.2 provides additional information."

 

[BAretired]

Two concentrated loads symmetrically placed on beam.

BA

 

[r13]

I found something from the Masonry Society. The equations for shear design and allowable stress are listed on p.19-20. Also, there is an example utilizing M/(V*d[sub]v[/sub] to determine F[sub]v[/sub]. I don't think this document answers your question in direct manner, but it might help to read through the example with code by your side. Link

 

[r13]

BAretired and KtootK,

After a quick glance into the paper I linked, my impression is the term M/(V*d[sub]v[/sub]), or shear span ratio, is used in equation to determine the allowable shear stress of a plane in a cantilever masonry wall (maybe valid for simply supported wall as well). M and V are the calculated forces on that plane, and d[sub]v[/sub] is the length of that plane in direction of the shear force (beam depth). The limiting shear span ratio was determined by researches, and is best kept at less than or equal to 1.0, to minimize the allowable stress, though the ratio could be much higher than 1.0. The design method is ASD based, so the conservativism. I am not a masonry guy, if I made mistake, please advise. Thanks.

 

[BAretired]

retired13 and KootK,

I am not a masonry guy either, but the whole notion of assuming the value of M/(V*dv) to be 1.0 seems bizarre to me; however, I have not studied the research that went into the design recommendations, so it's probably best that I keep my opinions to myself.

The limiting shear span ratio was determined by researches, and is best kept at less than or equal to 1.0, to minimize the allowable stress, though the ratio could be much higher than 1.0. The design method is ASD based, so the conservativism. I am not a masonry guy, if I made mistake, please advise. Thanks.

I do not think I agree with your conclusion. If the value of M/(V*dv) is permitted to be greater than 1.0, the expression for Fvm would be reduced, not increased (see below).

Fvm = 0.5[4.0-1.75(M/(V.dv))].sqrt(f'm)+0.25(P/An).

BA

 

[r13]

BA,

Yes, agreed.

 

[BAretired]

As a matter of fact, if we take the calculated value of 2.0 for M/Vdv, fv is greater than Fvm (see below).

BA

 

[r13]

Some interesting notes.

- ACI concrete shear equation, note the familiar term Vu*d/Mu.

This shear strength may also be computed by the more detailed calculation for members subject to shear and flexure only:

Vc = 1.9*sqrt(f'c)*b[sub]w[/sub]*d + 2500*ρ[sub]w[/sub]*Vu*d/Mu

....., Vu*d/Mu should not be taken greater than 1.0, and Mu is the factored moment occurring simultaneously with Vu at the section under evaluation.

-

The shear strength of deep beams is predominantly controlled by the effect of shear stress. These beams have a small shear span/depth ratio, a/d .... See Fig. 5 and Table No. 1 for classification of beams as a function of beam slenderness (Shear Span/Depth Ratio as a Measure of Slenderness).

Table No. 1 classifies the beams as:

a/d > 5.5 [Slender] - Failure mode: flexural
2.5 < a/d < 5.5 [Intermediate] - Failure mode: diagonal tension
1.0 < a/d < 2.5 [Deep] - Failure mode: shear compression

Any thinking, coimment?

 

[BAretired]

If Vu*d/Mu should not be taken greater than 1.0, then it can be less than 1.0, in which case, Mu/Vu*d can be more than 1.0.

BA

 

[Settingsun]

It looks more and more like shear capacity enhancement near a support for a slender beam, or capacity increase due to flattened strut angle for squat walls (deep beams).