Joel_Lapointe
Mechanical
I have a stress state that gives a sign of zero for the signed von Mises stress.
According to most of the literature, the sign is coming from the first invariant I1 of the stress tensor (Hydrostatic stress):
For the general stress state the invariants are :
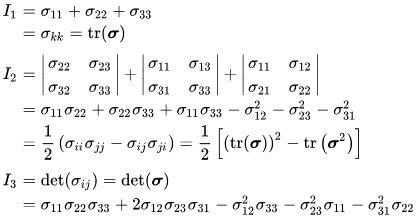
For the principal stresses the invariants are :
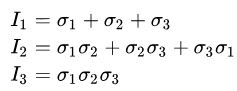
The first invariant allows for the sign to be zero. People do add in very small number (e.g. 0.000001) to remove the zero case. I don't like this gerrymandering.
Is it acceptable to use the other 2 invariants instead? Their signification might be totally different hence unusable?
Thank you...
According to most of the literature, the sign is coming from the first invariant I1 of the stress tensor (Hydrostatic stress):
For the general stress state the invariants are :
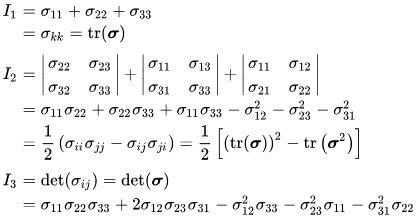
For the principal stresses the invariants are :
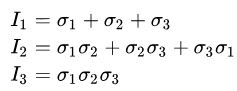
The first invariant allows for the sign to be zero. People do add in very small number (e.g. 0.000001) to remove the zero case. I don't like this gerrymandering.
Is it acceptable to use the other 2 invariants instead? Their signification might be totally different hence unusable?
Thank you...
